User talk:Ancheta Wis/t
Early life and academic career[edit]
He was born in Tui, Galicia, a part of the diocese of Braga, Portugal. He was baptized into the Catholic faith on 25 July 1551,[1] to António Sanches, also a physician, and Filipa de Sousa[2]. Being of Jewish origin, even if converted, he was legally considered a New Christian by the laws of Portugal and Spain at that time. In 1550, the French king Henry II granted letters patent to all New Christians who moved to a French city to start a business. The brother of António Sanches, Adam-Francisco Sanches, thereupon moved to Bordeaux, France; António Sanches followed the example of his brother by moving from Portugal to Bordeaux in 1562.
Francisco Sanches studied in Braga until he was 12 years old, when he and his parents escaped the surveillance of the Portuguese Inquisition. Sanches continued his studies at the College de Guyenne from 1562 to 1571.Cite error: A <ref> tag is missing the closing </ref> (see the help page). as the analog quantities.
Centrally, these analog systems work by creating electrical analogs of other systems, allowing users to predict behavior of the systems of interest by observing the electrical analogs.[3] The most useful of the analogies was the way the small-scale behavior could be represented with integral and differential equations, and could be thus used to solve those equations. An ingenious example of such a machine, using water as the analog quantity, was the water integrator built in 1928; an electrical example is the Mallock machine built in 1941. A planimeter is a device which does integrals, using distance as the analog quantity. Unlike modern digital computers, analog computers are not very flexible, and need to be rewired manually to switch them from working on one problem to another. Analog computers had an advantage over early digital computers in that they could be used to solve complex problems using behavioral analogues while the earliest attempts at digital computers were quite limited.
Some of the most widely deployed analog computers included devices for aiming weapons, such as the Norden bombsight[4] and the fire-control systems,[5] such as Arthur Pollen's Argo system for naval vessels. Some stayed in use for decades after World War II; the Mark I Fire Control Computer was deployed by the United States Navy on a variety of ships from destroyers to battleships. Other analog computers included the Heathkit EC-1, and the hydraulic MONIAC Computer which modeled econometric flows.[6]
The art of mechanical analog computing reached its zenith with the differential analyzer,[7] built by H. L. Hazen and Vannevar Bush at MIT starting in 1927, which in turn built on the mechanical integrators invented in 1876 by James Thomson and the torque amplifiers invented by H. W. Nieman. A dozen of these devices were built before their obsolescence was obvious; the most powerful was constructed at the University of Pennsylvania's Moore School of Electrical Engineering, where the ENIAC was built. Digital electronic computers like the ENIAC spelled the end for most analog computing machines, but hybrid analog computers, controlled by digital electronics, remained in substantial use into the 1950s and 1960s, and later in some specialized applications. But like all digital devices, the decimal precision of a digital device is a limitation, as compared to an analog device, in which the accuracy is a limitation.[8] As electronics progressed during the 20th century, its problems of operation at low voltages while maintaining high signal-to-noise ratios[9] were steadily addressed, as shown below, for a digital circuit is a specialized form of analog circuit, intended to operate at standardized settings (continuing in the same vein, logic gates can be realized as forms of digital circuits). By the time of the Space race to the Moon, the Apollo Guidance Computer was successfully constructed from 41 hundred NOR gates using the RTL logic family of integrated circuits. But as digital computers have become faster and use larger memory (for example, RAM or internal storage), they have almost entirely displaced analog computers. Computer programming, or coding, has arisen as another human profession.
While trying to track down a Stanovich 2007 citation, I found Stanovich, Keith E. (2007). How to Think Straight About Psychology. Boston: Pearson Education. I am not conversant with this author or his citation, so I commented out its sentences, and would appreciate it if another editor could verify the citation for the benefit of the article. --Ancheta Wis (talk) 02:47, 17 April 2011 (UTC)
But in the meantime, I found that some citations from Thomas Brody, Imre Lakatos, and Goldhaber and Nieto have been commented out. These sources are perfectly good. To demonstrate this, I list relevant quotations and their citations, which have been commented out, for some reason. --Ancheta Wis (talk) 02:47, 17 April 2011 (UTC)
Some background:
- Ludwik Fleck (1935, translated into English 1979) Genesis and Development of a Scientific Fact University of Chicago Press ISBN 0-226-25325-2 Chapter Two:"Epistemological Conclusions from the Established History of a Concept" pp.20-41.
- Fleck is as important as Karl Popper (author of Logic of Scientific Discovery), in the estimation of Thomas Kuhn (author of Structure of Scientific Revolutions), who wrote the June 1976 foreword to the 1979 translation of Fleck; Fleck's concepts are complementary to Popper's views (even as these views evolved during Popper's lifetime). Fleck's starting point is that science is too large a subject for a single mind, and his thesis is that scientific progress depends on communities, which he styles thought collectives (Denkkollektiv). Fleck describes the development of the thinking style (Denkstil) of these communities. Fleck emphasizes that even the terminology in a scientific inquiry is rooted in the problem at hand, however poorly the terminology is formulated in the beginning. As the understanding of a problem is reformulated, its terminology stabilizes and usage in that scientific community promulgates and propagates the thought style of that specific community.
- Pages 27-8: "In the history of scientific knowledge, no formal relation of logic exists between conceptions and evidence. Evidence conforms to conceptions just as often as conceptions conform to evidence. After all, conceptions are not logical systems, no matter how much they aspire to that status. They are stylized units which either develop or atrophy just as they are or merge with their proofs into others."
- Thomas Brody, The Philosophy Behind Physics Springer-Verlag p.45: "scientific theories evolve and change" (Even between the revolutionary phases posited by Kuhn)
- Imre Lakatos, Proofs and Refutations Cambridge University Press p.126: "Epsilon: really, Lambda, your unquenchable thirst of certainty is becoming tiresome! How many times do I have to tell you that we know nothing for certain?"
- Alfred Scharff Goldhaber and Michael Martin Nieto (23 March 2010) "Photon and graviton mass limits" pp. 939-979 Reviews of Modern Physics 82 January-March 2010: pp 940-1 -- "The canonical view of theory testing is that one tries to falsify theory. ... [A] theory can earn trust in three ways ... First, a striking, even implausible prediction is borne out by experiment or observation ... [Second], people see ways to apply the idea in other contexts. ... [Third] if many closely related subjects are described by connecting theoretical concepts, then the theoretical structure acquires a robustness which makes it increasingly hard - though certainly never impossible - to overturn."
One of the comments hidden in the article cites Kierkegaard without further information, apparently the basis for commenting out the citations. --Ancheta Wis (talk) 02:47, 17 April 2011 (UTC)
- Andrew Lancaster, rather than add another flavor of the myriad philosophical positions, it may be helpful to use the guidelines of summary style. So a table, showing the genetic relationship of the philosophical positions, might replace the large contribution we are currently enjoying from rtc. In its stead, the summary style guidelines might serve as the rules of engagement for futher enlargement of the section. As the summary style guidelines state, as the main article grows organically (ala rtc's contribution), subpages are spawned from it, replaced by summaries. Perhaps we might take advantage of the cross-cutting style which allows us to contrast the current widely-ranging statements side-by-side at a 50,000 foot view. Then hyperlinks can lead interested readers to the subpages.
- My difficulty with more text on positivism is that it forked from empiricism, beginning in the 1920s, and more or less died in the 1940s along with Otto Neurath's contribution to the failed International Encyclopedia of Unified Science. Neurath's monograph was a companion to Kuhn's Structure of scientific revolutions. The entire project never went anywhere; Kuhn was definitely a success, in contrast to positivism.
- Perhaps Popper's categorical statements on theory are meant to apply to philosophical theory rather than scientific theory. Popper is actually understandable if this interpretation is taken, as scientists like Feynman were actively antiphilosophical. --Ancheta Wis (talk) 21:15, 14 January 2011 (UTC)
Peirce's triads[edit]
Tetrast, while sorting through quotidian items, I noticed that Peirce's triads have an unexpected utility for me. It may logical to posit a binary proposition P, but P may or may not fit the real world: P, not P, and '?huh?' which Sowa alludes to in 'Thirdness' (see the link above). The size of a third category is a commentary about the fitness of P to be a proposition about the real world. In other words, P may or may not be a worthy hypothesis for consideration. A third category allows room for doubt, which of course is the beginning of knowledge for Peirce. --Ancheta Wis (talk) 14:45, 17 October 2010 (UTC)
Possible directions for development[edit]
I was actually working on ARM-related points when the merge tag was added; currently the ARM-based OSs allow for faster boot times, for event processing that was specialized for fingertip events, and for increased battery life. The legacy OSs basically ignored these design decisions and it will be some time before they are added. Windows CE allowed for ARM processors, but apparently this was incompatible with Windows as it then stood (as of January 2010). Now that MS has seen the consequences of the legacy decisions, MS has purchased an ARM architecture license to redress this. Again it will take time for the rework to be completed. See the Windows 8 citation in the article (i.e., release in 2012). Event processing is one area where QNX has a competitive advantage. --Ancheta Wis (talk) 01:18, 8 October 2010 (UTC) --edited Ancheta Wis (talk) 12:34, 11 October 2010 (UTC)
In retrospect, the division between the camps is desktop legacy versus untethered target systems for deployment. Since desktop is one billion PCs, apparently this outweighed the small team for tablets. Witness the cancellation of WinCE-based Microsoft Courier project. It remains to be seen how much the proof of concept OS kernel MinWin will get into the reworked OSs for tablets. There may not be enough development time to outweigh the competitive advantage of getting to market in enough time to make a difference with the competition, which is not static, but also changing. Witness Motorola, which could not afford the time required for MS to overcome the legacy software inertia. --Ancheta Wis (talk) 01:29, 8 October 2010 (UTC)
There were other concepts which MS scrubbed. For the fundamentals which Apple understands, see Don Norman, Design of Everyday Things. As you can see, this went beyond the classic PC concept several decades ago. See especially Don Norman's '7 stages of action' in the pdf. --Ancheta Wis (talk) 03:15, 8 October 2010 (UTC)
- It appears that the designer behind the Windows Phone 7 UX (user experience -- he apparently started tiles, which are user-definable icons -- and hubs, which aggregate apps) talked in Feb 2010 --Ancheta Wis (talk) 11:03, 11 October 2010 (UTC)
While the merge discussion is proceeding, I propose to continue my search for citations in the direction outlined above. OK? --Ancheta Wis (talk) 14:56, 8 October 2010 (UTC)
Computer program linking and loading[edit]
The personal computer model obeys the time-honored model of computer program development begun in the 1940s. I here argue that a tablet computer has forced upon us a retail/wholesale divide in that model. Specifically the program load step in computer program development needs to be examined in more detail to show that these steps still exist in tablet computer program development. From a programmer's POV, program load is unchanged for either tablets or PCs. Namely, that a program loader deploys the bytes of an executable file from a storage area (whether it be Solid State Disk, USB external drive, Read-Only Memory, or other source of data) in order, onto program memory to be consumed in a fetch-execute cycle.
How does this traditional (i.e., PC) load process differ from program load on a tablet computer? First of all, as Vyx has steadfastly reminded us, a tablet computer executes a program which is not wholly under the control of a single mind, in principle. A vendor of a tablet holds a retail key which, unless delegated to a programmer, controls program load. This retail key has been implemented in different ways by different vendors, who seem to have evolved their respective implementations in response to their individual urges to survive as entities. What I mean is that Apple's retail key to program 'load and go' (an IBM buzz-phrase which I coopt) is membership in their App Store, which Vyx has kindly reminded us costs a programmer $$$. Google's retail key is more distributed, but even program membership in Android Market is not automatic, but requires their permission. The MS retail key is somewhat intermediate, $$ for membership, etc.
What does this loss of wholesale freedom to an individual programmer buy us (the general non-programming public)? I think of it as the difference between the electric starter and the hand-cranked starter for an automobile. With this invention, women could insert a retail key into an ignition, start cars and drive autonomously. In other words, tablets are not just for programmers to do with as we please, but are tools and appliances for us to use conveniently on a daily basis. They just happen to be computers which will cannibalize the existing market for all programmers, but also liberate the rest of us when computing tools free us from having to remember dates, times, dollars, appointments, faces, tunes, etc. thereby making us collectively smarter.
But for the editors who ask "... and your point is?" I am asking that we lay down our arms and work on the article.
If the response is "but there will be a tablet vendor who will make it completely open." my response is that the existing vendors are attempting to maintain a critical mass which is observably larger than one enabled by the open model. It is observably true that a retail component is needed to make them succeed. It is observably true that a completely open enterprise will not be profitable in the short term. I agree that this statement remains to be proven. But we will not know for several years. I predict that this statement will be shown to be true. --Ancheta Wis (talk) 03:04, 13 October 2010 (UTC)

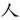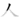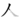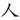 , Chinese: rén, Korean: in, Japanese: hito, nin; jin). The character has two strokes, the first shown here in dark, and the second in red. The black area represents the starting position of the writing instrument.
, Chinese: rén, Korean: in, Japanese: hito, nin; jin). The character has two strokes, the first shown here in dark, and the second in red. The black area represents the starting position of the writing instrument..
- ML, as an American, I see similarities between Lee Kuan Yew and Abraham Lincoln. Both were attempting to save their polities, one forced by history to unite his polity into a city-state, the other forced by history to unite a confederation (think Switzerland) into a republic (think Roman Republic). If you see difficulties including issues like this in the article, that is more evidence that the studies of the humanities are not of the same type as the studies of the hard sciences. If the position is that these sets of topics enjoy the study of a common underlying type, then perhaps that common type might be included. I believe that is what Peirce was discussing in the bulleted lists from Tetrast. It may be too much to hope that someday the publications of some researcher will unite a formerly disparate mass of facts about the social sciences into theorems of a larger science, as the American Josiah Willard Gibbs did for chemical engineering. I can think of the writings of some candidates (which I may not disclose by the rules of Wikipedia). --Ancheta Wis (talk) 03:40, 7 October 2010 (UTC)
Kenosis, I have been thinking about how to phrase a lede (no, not the lede of this article) so that a 3rd grader could understand it. As I understand it, first and second graders can read sentences, add and subtract numbers, sit quietly, and play well with others. Please correct me if I am completely wrong. A third grader is learning how to multiply by rote, can compose grammatical sentences, and perhaps learn some facts about the world.
A seventh grader learns about state history, some algebra, some science, some geography, some science. The New York Times attempts to write articles at seventh grade level.
So here goes:
Science is about 'reliable knowledge' — things you know you can depend on about our world. People have been studying science for thousands of years — since before people knew how to write, when people only talked about things, and also showed each other how to do things, with pictures and paintings, with songs and dances, and with customs - things that your parents did, and their parents did before them, and their parent's parents did before them, and more, 100 sets of parent's parent's ..... (repeat 100 times) parents did before them. That was so long ago that the world was different then, with different animals, with different rivers, shorelines, and deserts, grasslands, and forests than we have today. Science is also about how things will be in a future time, say in a time when your children's children's .... (repeat 100 times) children will be, after you.
Can there be things that we know were true so long ago, and which will be true so long from now? Scientists, the people who figured out our science, say 'yes', because what we know all fits together. What we know is not about secrets, but is about what we can all know now.
Then why can't we just learn these true things, here, now? Why do we have to keep going to school? Because there is too much to know. The most complicated things we know are far more complicated than what we can remember — seven things at one time. Most of the time, we have to depend on each other to set up things so that we can do our jobs in the best way we know how — and each of us is different from the other people around us — with different talents and different weaknesses. So we go to school to learn what we do best, and to learn how best to depend on each other.
Most importantly, we need to learn how to learn, so we can keep learning for the rest of our lives.
Thousands of years ago[edit]
Our world had far fewer people. People mostly lived by hunting other animals and gathering plants. People could weave nets together to catch and hold what they wanted. People lived in small groups and only trusted those in their group.
Thousands of years from now[edit]
We cannot be absolutely certain, but we can make estimates:
Stable number of people[edit]
The world stabilized in year 2050 at 9.5 billion people, when industrialization reached all continents of the world.
Shrinking number of people[edit]
The world continued its lifestyle improvement, which required that our economic systems continued consolidation of capital.
Expanding number of people[edit]
People continued colonization of the unsettled portions of the world: the oceans, the deserts, the mountains, Antarctica, and under the sea.
Wobbling number of people[edit]
World systems will grapple with issues and the population will rise or fall with available capital.
In the article on scientific method, we were asked to include a quote from Imre Lakatos into the section for the relationship with mathematics; in the search for a suitable quote, I was drawn into study of Lakatos' Proofs and Refutations, which uses an example from George Pólya's Mathematics and Plausible Reasoning, the Euler characteristic. The Euler formula V − E + F = 2 originally applied to polyhedra, with vertices V, edges E, and faces F; in the century after publication, various counterexamples (monsters) were found and buried until it was understood that 2 was not always the result to be expected when the objects studied were not the classic Greek solids.
Before his untimely death, Lakatos came to view the search for proof as a vehicle for 'dominant theories' (such as logic, or statistics, or computer science etc). Science, of course, is itself a dominant theory.
(So far, the best quotation I have found was
- "Epsilon: Really Lambda, your unquenchable thirst for certainty is becoming tiresome! How many times do I have to tell you that we know nothing for certain? But your desire for certainty is making you raise very boring problems — and is blinding you to the interesting ones. — Proofs and Refutations p. 126
) -- Note Lakatos' technique of using characters with different voices, like Galileo in Two New Sciences, so that he can juggle POVs.
- @Eraserhead1, @Vyx, @Mahjongg, @Snottywong, Vyx asked me to contribute: There is at least one other issue. (Vyx, I would appreciate it that you please not interpolate comments into this contribution, until after my signature)
- 3: control of the target's system software, where the terms are defined in a debate which erupted on this page just after the iPad announcement. I am using Apple as the exemplar.
- To a consumer, the target system software is defined by the source of the target device, in this case, Apple.
- From Apple's POV, the iPad is an expression of Apple's intellectual property, which gives Apple a claim on the control of the iPad's system software, and to Apple, control of the vendors for its Application software market. It appears that from Vyx's POV, the intervening 'computer operator', for example, the guy in charge of inserting the punch card deck into the card reader of the mainframe, is the gatekeeper for the software being run on the mainframe in behalf of the programmers, and that the defining difference for a personal computer is that the punch card gatekeeper, the application programmer, and the user are one and the same person, as opposed to the mainframe case. Now for Apple, the gatekeeper is implemented by a whole ecology of software - what I am glibly calling the system software, but which in today's world is implemented by an IDE, a development host, a programming language, an operating system, and a deployment process to a target -- the iPad.
- Before the afore-mentioned debate, I did not appreciate that Apple has found a 'sweet spot' in the possible environments for developing software. What I mean is that if Apple retains control of the entire process all the way to the point of deployment, (ie. from a PC POV, all the way to the Windows Installer ), then it is possible to manage complexity in an appealing way. --Ancheta Wis (talk) 14:57, 17 September 2010 (UTC)
The following year, 1638, Galileo published his landmark experiments in Two New Sciences.[10]
- For a US-centric view -- In physics, try Reviews of Modern Physics; in general science, especially biology, and anything that would be of interest to all scientists, see Science (journal). You wouldn't go far afield to read the overview articles of the encyclopedia either. There is too much to cover, however, and it would be a disservice to the specialties to attempt a synoptic view of the state of the art of all the speculations, hypotheses and wild, currently discredited guesses that don't pop up in commentary until there is some sort of evidence for them. For example arXiv has everything that a suffiently brave researcher can throw at it; but one's reputation (and future) are on the line, in that case. --Ancheta Wis (talk) 17:56, 21 June 2010 (UTC)
Simplicity[edit]
I undid a good faith edit (as omitting the subtleties in the treatment of electron in material) on the following grounds:
- the thought processes are well known. They have been used to describe materials (e.g. gases, crystals to name the simplest cases) with decades of history (sometimes centuries of history).
- if we can't discuss simple cases first, but are constrained to the most general first, then we are ignoring the examples of Galileo, Newton, Bohr, Dirac etc.
- if we can't talk about something as simple as an electron, then we are ignoring items with literally centuries of background.
At its base, Physics can be simple. If there is something I have learned from my teachers, it is at least this. And that includes several Nobel laureates, who were quite clear about the need NOT to obfuscate what can be simple; to do otherwise, in fact is dishonest. --Ancheta Wis (talk) 01:52, 29 March 2010 (UTC)
I am trying to find a good article to point to from the history of computing hardware. As I am sure you all know, quantum computing elements rely on physical systems with a repeatable set of known states, regardless of the current value of each state. Hence spin up/down, cat dead/alive etc. In the Haskell (programming language), it is not even necessary to resolve a value until the result of a computation is required, by allowing each potential calculation to be wrapped up in chunks (or thunks), to be resolved only when it is absolutely necessary. Thus infinities can be neatly manipulated without fear of overflowing physical registers, in this kind of language.
Hence my request; I need an article which contains the point that there are physical systems which are well-known (i.e., not a muddle) and which ultimately resolve to real physical situations (spin up/down etc). Then in the computing hardware article, I can then simply reference the link.
It won't work to use the double-slit experiment because the presence/absence of diffraction is not a reliable-enough (ie. digital-enough) situation. It won't even work to use the quantum Hall effect because
- This might not be your setup. I recall seeing these symptoms years ago and dismissed them as database lag. Have you correlated these symptoms with the time of day, or with the times of database backup? (I admit I now have 2GB of memory and back then I had 1 GB or perhaps less, & I too upgraded to FF6, just now. So just because I see no side-effect, this is no guarantee of no FF bug somewhere) --Ancheta Wis (talk) 22:17, 15 March 2010 (UTC)
This phrase comes from Needham (2004) Science and Civilisation in China Vol 7 part 2, page 84, "China's Immanent Ethics": wei jen min fu wu! (為人民服務! In everything you do, let it be done for the people). The next sentences state "(in some future incarnation) ... I should pray for Chinese colleagues, the descendants of the sages, with their sense of justice and righteousness (liang hsin 良 )"
I notice that the characters from Needham are not the same as a very similar attribution to Mao. Doubtless Needham transcribed and translated this after hearing it verbally. --Ancheta Wis (talk) 01:34, 11 March 2010 (UTC)
Needham, Robinson & Huang 2004, p.218
Needham et al. 1986, p.x
- Needham, Joseph; Wang, Ling (王玲) (1954), Science and Civilisation in China, vol. 1 Introductory Orientations, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph; Wang, Ling (王玲) (1956), Science and Civilisation in China, vol. 2 History of Scientific Thought, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph; Wang, Ling (王玲) (1959), Science and Civilisation in China, vol. 3 Mathematics and the Sciences of the Heavens and the Earth, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph; Wang, Ling (王玲) (1962), Science and Civilisation in China, vol. 4 Physics and Physical Technology part 1 Physics, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph; Wang, Ling (王玲) (1965), Science and Civilisation in China, vol. 4 Physics and Physical Technology part 2 Mechanical Engineering, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph; Wang, Ling (王玲) (1971), Science and Civilisation in China, vol. 4 Physics and Physical Technology part 3 Civil Engineering, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph; Lu, Gwei-Djen (1974), Science and Civilisation in China, vol. 5 Chemistry and Chemical Technology part 2 Spagyrical Discovery and Invention: Magisteries of Gold and Immortality, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph; Ho, Ping-Yu; Lu, Gwei-Djen (1976), Science and Civilisation in China, vol. 5 Chemistry and Chemical Technology part 3 Spagyrical Discovery and Invention: Historical Survey, from Cinnabar Elixirs to Synthetic Insulin, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph; Lu, Gwei-Djen (1980), Science and Civilisation in China, vol. 5 Chemistry and Chemical Technology part 4 Spagyrical Discovery and Invention: Apparatus and Theory, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph; Lu, Gwei-Djen (1983), Science and Civilisation in China, vol. 5 Chemistry and Chemical Technology part 5 Spagyrical Discovery and Invention: Physiological Alchemy, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph; Tsien, Tsuen-Hsuin (1985), Science and Civilisation in China, vol. 5 Chemistry and Chemical Technology part 1 Paper and Printing, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph; Ho, Ping-Yu; Lu, Gwei-Djen; Wang, Ling (王玲) (1986), Science and Civilisation in China, vol. 5 Chemistry and Chemical Technology part 7 Military Technology: The Gunpowder Epic, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph; Lu, Gwei-Djen (1986), Science and Civilisation in China, vol. 6 Biology and Biological Technology part 1 Botany, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph (1988), Science and Civilisation in China, vol. 5 Chemistry and Chemical Technology part 9 Textile Technology: Spinning and Reeling, Cambridge University Press
{{citation}}:|first2=has numeric name (help);|first2=missing|last2=(help); Invalid|ref=harv(help) - Needham, Joseph; Bray, Francesca (1988), Science and Civilisation in China, vol. 6 Biology and Biological Technology part 2 Agriculture, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph; Yates, Robin D.S. (1994), Science and Civilisation in China, vol. 5 Chemistry and Chemical Technology part 6 Military Technology: Missiles and Sieges, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph; Harbsmeier, Christoph (1998), Science and Civilisation in China, vol. 7 The Social and Economic Background part 1 Language and Logic, Cambridge University Press
{{citation}}: Invalid|ref=harv(help) - Needham, Joseph; Robinson, Kenneth G.; Huang, Jen-Yu (2004), Science and Civilisation in China, vol. 7, part II General Conclusions and Reflections, Cambridge University Press
{{citation}}: Cite has empty unknown parameter:|1=(help); Invalid|ref=harv(help)
I would like to put in a little plug for Hueco Tanks in El Paso County, Texas about 30 miles NW on on Montana avenue from EP the city. There are Hopi-style masks painted on some of the cave walls but the modern Hopi who come to visit no longer can speak to their meaning. There are paintings of Corn Tassels (which would have given the sacred corn pollen) and Corn Flowers (which is an Aztec food ingredient). There are nopales (prickly pear) in abundance for the eating, to this day. There are paintings of Tlaloc and Quetzalcoatl. I put in the citations in the article. The people of EP feel kinship (Puebloan, Aztec, Apache, Kiowa (& perhaps Wichita?) Spanish, Anglo) with the markings on the cave walls. You can see the various ancestries in the populace today obviously.
Oh, did I mention the folsom point which was found at Hueco tanks? That says the region has been inhabited since 10-12 000 years ago, just about the time the megafauna went extinct. I know for a fact that a ground sloth was found in a lava tube at Aden crater, several miles north of Kilbourne hole and 60 miles west of Hueco tanks. That fits in nicely with the folsom point. --Ancheta Wis (talk) 20:13, 3 March 2010 (UTC)
Needham (1956), Science and Civilisation in China] vol 2 History of Scientific Thought 697pp, on page 173 discusses Mohist fa, from 4 parallel resources:
1) Than Chieh-Fu (ed.) Mo Ching I Chieh, Analysis of the Mohist Canon. Com Press (for Wuhan University), Shanghai, 1935. Needham abbreviates this source as Cs.
2) Fêng Yu-Lan, "Yuan Ju Mo" On the Origin of the Confucians and Mohists Chhing-Hua Hsüeh-Pao (Tsinghua University) Journal 1935 10 279.
3) Fêng Yu-Lan, '
- In case you need this, I always feel better when I hear Elmer Bernstein (1962), Theme from To Kill A Mockingbird. The reference to mockingbirds is that they hurt no man, and only sing to us. --Ancheta Wis (talk) 16:34, 19 February 2010 (UTC)
- Well, here is a disconnect. When I read the description before I was seeing it statically. But if your concept is a flow from two corners to the top, then this picture does not follow from the words which I read. Logically, there could also be a flow from genetic & personal to cultural. I would visualize this as a flow in another direction than from bottom to top. But thinking about it, I can envision the two bottom corners converging in the center and then flowing to the top. What this flow could symbolize might be an enculturated individual changing perception due to his/her personal experience. Other flows, say from top corner merging with genomic expression might symbolize the learning experiences of an individual, flowing to the culture corner, influencing his/her culture (a form of leadership). Yet another kind of flow might be top corner merging with culture, flowing to the genomic expression corner might symbolize gene flow (effect on marriage & family). --Ancheta Wis (talk) 20:05, 18 February 2010 (UTC)
- Well, I can't help the feeling of revulsion. It would be quite as revolting as eating a stew and finding monkey hand inside it (i.e., it would look like human baby hand).
- Nobel Memorial Laureate Herbert Simon, in his 1991 autobiography Models of My Life recounts his perception of sudden emotional coldness from his hosts at a dinner party, who were as urbane and understanding as he; the precipitating event was his positing a thought experiment, of raising a robot with artificial intelligence (which was dear to his heart, as one of the founders of the science) as a human child; his hosts reacted with coldness; Herbert Simon hastily back-pedaled. --Ancheta Wis (talk) 08:29, 13 February 2010 (UTC)
- Simon, p. 312 writes of "a gleam of understanding over my driver's face" when Simon posed a question about ethnicity in Peru.
- I think the point is to arose that gleam of understanding over the Internet without having the feedback of speaking face-to-face. --Ancheta Wis (talk) 08:54, 13 February 2010 (UTC)
- Simon, p. 152 writes how Elliott Dunlap Smith's role-plays (as teaching devices) indelibly taught how we reveal ourselves to others. In other words, we ourselves control how others will come to see us. --Ancheta Wis (talk) 09:03, 13 February 2010 (UTC)
Type (model theory) was recently removed from See also; I can see its use as a way to abstract the grammar of statements about types. In that sense, it is related to the other Type articles as a container or context. Some semantics (of client theories) can be documented this way. --Ancheta Wis (talk) 15:42, 12 February 2010 (UTC)
- Damir Ibrisimovic, it's different from Stanford Encyclopedia of Philosophy, or Citizendium. Wikipedia's tradition is that everyone is an administrator of the article, and everyone is editor of the article. No one is given any currency except that afforded by the immediate circle of editors of the current article under the searchlight. So if the article became too 'hot', the buzz would attract more editors in a positive feedback loop, until the cumulative changes fall of their own weight, and the article then sinks back into quiescence. But if an editor were to violate some policy, then the entire weight of the encyclopedia falls on the hapless editor and no one can save him. Thus editing the encyclopedia treads a fine line which depends entirely on the readership of that article.
- To all editors:
- I propose to archive a subset of the talk page as denoted above. If there are any specific talk threads which any editor wishes to leave un-archived, please respond here. I will wait one week. In the meantime, the talk page will continue to serve as a waystation for improvement of the article. --Ancheta Wis (talk) 23:17, 9 February 2010 (UTC)
When I came across this concept, I was confused: does the adjective 'Franco-' refer to a political entity, a temporary alliance, a pejorative, ... what? It appears to refer to a still-controversial topic or to a possible historical event which is yet to be proven.
The slant which disturbed me is that to me, 'Franco-' is not the same as 'Frankish-' or φράγκοι or Ferengi (in Hindustan). All of these appear to be names were was used to refer to the Franks, ie Frangistan, the land of the Franks, from an eastern POV, to what would possibly be referred to as France (That's what I associate with 'Franco-'). If that is so, then why is the article obscurely named? The Ferengi were the Crusaders of Christendom.
I now retreat to wait and read, but it is disturbing that the title of the article is Franco-Mongol alliance while the referents in the first paragraphs are denoted Franks. Why not call them Ferengi? Oh but wait, that name was hijacked by Roddenberry. --Ancheta Wis (talk) 13:18, 9 February 2010 (UTC)
- Your responses are revealing because they show that you have not considered that there can be computers without operating systems. The wildest one that has been mentioned to me was a two by four with notches in the corners to flip the rows of toggle switches, in order to start initial program load. I regret that I did not ask the name of the technician who thought of it. --Ancheta Wis (talk) 12:18, 1 February 2010 (UTC)
- I think it should be clear to you that in the future, when tablets are commonplace, that someone will use one to write a computer program which will be then executed by a blind CPU somewhere. OK? In fact people are doing that now on hosts which happen to be browsers for targets which also happen to be browsers (this alone shows that the programs need not be executed on a specified piece of hardware, such as a PC, because browsers just happen to be designed to be OS-independent). But that is not the purpose of the article which is on the verge of bursting forth out of this one. --Ancheta Wis (talk) 12:18, 1 February 2010 (UTC)
- To give an example which is not iPhone or Apple-centric: If there were some Android tablet (like the Barnes&Noble nook, for example) and some Android developer had already developed something (such as an astronomy application, to pull an example out of the air, such as the phase of the moon, for some vampire) to run on an HTC G1, for example, then all that developer would have to do to port his vampire's application to the nook would be to change 'size of the application display'. His targets were the G1 and the nook (the tablet computer) and his host development system would just have to be something that runs Java 6, Eclipse 3.5, and Android 2.1 (as we speak). His host could be a PC, a mac running an emulator, or a mainframe. To go even farther afield, his target could be an embedded system such as the chip on a greeting card starring Hoops and Yoyo or the chip on a smart card. --Ancheta Wis (talk) 04:30, 1 February 2010 (UTC)
- Yes, indeedee! By golly, I can even read, and I think am able to understand the English language! ..<<Dead silence here, followed by the tolling of faraway bells>>.. I also am not in the habit of ascribing or projecting the mental states of other sentient beings. According to this talk page, "Tablet PC" is trademarked by Microsoft. That alone justifies the page move, while we are on the subject of freedom. It even explains all the preemptive edits which systematically remove any references to iPad, now that I think about it. And no, I am not a mac person; I haven't even touched a mac in 21 years.
- According to this source, Microsoft Tablet PC software was available in 2003, but only to OEMs. How is that free and open?
- Here is a slate PC presentation from CES. Three Microsoft partners displayed. Pegatron showed a larger-screen display than Archos, who showed their personal media player under Windows 7. HP showed a slate running Kindle software which Ballmer held up and rolled a canned demo video. If we are talking openness and freedom, then why weren't the demos more 'live' than the iPad demo? What kind of POV is this? How free and unlimited is this? --Ancheta Wis (talk) 17:01, 31 January 2010 (UTC)
- Are you now supporting the notion of allowing iPad into this article? If not, then we ought to separate the redirect of tablet computer from this article, let the tablet computer article stand on its own, and put the category:tablet computer into the iPad article instead of the current category:tablet PC.
- Or might you support the notion of separating yet another article from this one: the slate PC. I see that it too is currently redirected to this very article. --Ancheta Wis (talk) 17:01, 31 January 2010 (UTC)
- I see that slate computer is currently a redirect to a section in this article. That section, which could conceivably encompass the iPad, is currently defining itself as a type of tablet PC. Will this change? --Ancheta Wis (talk) 17:01, 31 January 2010 (UTC)
- The HP Slate will be available sometime in 2010. According to this source, it was prototyped as an e-reader in the UK in 2005, and then improved from user feedback, and that the product could have been released 2 years ago for $1500, which is why HP has waited til now to demo it at CES. --Ancheta Wis (talk) 17:01, 31 January 2010 (UTC)
- It is only fair to point out that the category:tablet PC is not under discussion for the move. The presumption is that any eponymous category would be up for discussion in a different place than this page. But when a game-changer appears, it would be foolish to hold fast or ignore it. I should comment that Bill Gates predicted the success of the Tablet PC in 2001 with little result; it took a different set of players to create the ecosystem which enabled the imminent success of the Tablet computer.
- It may be more politic to separate the current redirect of Tablet computer to a separate article with a different agenda. The iPad article currently links to this one, which actually started the whole fracas.
- The action to sever the redirect would have the advantage of letting the editors of this article have their own space. The action to separate the names would allow another set of editors to create an entirely different one in peaceful coexistence (different article, different category, different class of device, as avowed by the current set of editors). Agreed?
- I propose to implement that change after the seven-day timer has expired for the current proposal.
In Haskell, "a function is a first-class citizen"[11] of the programming language. As a functional programming language, the primary control construct is the function; the language is rooted in the observations of Haskell Curry ( 1934, 1958, 1969) and his intellectual descendants, that "a proof is a program; the formula it proves is a type for the program".
- While searching for the requested quote I found this post in Proofs and Refutations:: "Many working mathematicians are puzzled about what proofs are for if they do not prove.... Applied mathematicians usually try to solve this dilemma by a shamefaced but firm belief that the proofs of the pure mathematicians are 'complete' and so really prove. Pure mathematicians, however, know better - they have such respect only for the complete proofs of logicians. [e.g. Hardy 1928]: 'There is strictly speaking no such thing as mathematical proof; we can, in the last analysis, do nothing but point; ... proofs are what Littlewood and I call gas, rhetorical flourishes designed to affect psychology, pictures on the board in the lecture, devices to stimulate the imagination of pupils.' ... G.Polya points out that proofs, even if incomplete, establish connections between mathematical facts and this helps us keep them in our memory: proofs yield a mnemotechnic system [1945]. - p.31- 32 BETA: Not 'guesswork' this time, but insight! TEACHER: I abhor your pretensions 'insight'. I respect conscious guessing, because it comes from the best human qualities: courage and modesty. - p.32 "
- First, I would like to thank the anon 93.86.x.y for leading me to Lakatos, Worrell and Zahar (1976), Proofs and Refutations: the logic of mathematical discovery Cambridge ISBN 0 521 21078 x Parameter error in {{ISBN}}: invalid character, which is a very pleasant read. I have found some candidate quotations which I am asking the editors of this article to select from:
- p.
- I like your changes, but I can't understand why "The monad acts as a framework" isn't part of the lede sentence instead of the familiar "abstract data type" phrase. It is too easy for a standard C++ programmer to read the familiar phrase and get completely misled, because the whole monad concept is post-imperative (read: it will take study and a commitment to learn a whole new set of concepts, first).
- For the historically minded, a Eugenio Moggi article would have helped. But it doesn't exist yet. I personally recommend Gordon's thesis Functional Programming and Input/Output for background.
- Since functions are the only control construct in functional programming,
- Marax, It may be helpful to reread about Bacon's idols. --Ancheta Wis (talk) 11:30, 23 October 2009 (UTC)
- And just to be clear, all I mean about induction is the standard viewpoint:
| Induction | Deduction | |
|---|---|---|
| 1 | Start from a case | Start from a general statement |
| 2 | Examine the particulars of that case | Give a specific example of the general, as a type |
| 3 | Repeat, next particular, find commonality | Explicate the type, in propositions |
| 4 | Generalize to the collection as a type | Give expected result for that type |
- As the type of anything is the heart of a scientific statement, it is a reflection of the judgement of the investigator. It selects what is important or crucial about the proposition.
- For example, in Newton's theory, a mass is a property of some object. In this case, the mass of that object allows a statement about any other object of the same type (e.g., mass points, rigid bodies, fluids etc.)
- As another example, a physician can be considered to be an expert in health issues. In this case, the expertise of the physician can be typed: good, expert, quack, etc.
- In Maxwell's theory, charge is the relevant base type.
- In finance, the cash position is the basic.
- My favorite is the private soldier in The Dirty Dozen, each of whom rehabilitate themselves, by personal heroism, as worthy of a general discharge as an ordinary soldier (as a type).
- Naturally, it is a conceptual error to confuse the general statement in deductive reasoning as a causal statement. For example "all physicians are experts".
- None of this is new. --Ancheta Wis (talk) 13:32, 2 October 2009 (UTC)
- On the face of it, the sentence "His methods of reasoning were later systematized by Mill's Methods" is an oversimplification. If it were true, then we would be able to find a citation. I propose commenting out the sentence until the originating editor can give a citation.
- --Ancheta Wis (talk) 03:36, 1 October 2009 (UTC)
--Ancheta Wis (talk) 23:19, 30 September 2009 (UTC)
- I have an idea: what if there were another section, say Reprise -
Proposed beginning for a new section: Reprise[edit]
"Truth is sought for its own sake ... Finding the truth is difficult, and the road to it is rough. For the truths are plunged in obscurity. ... God, however, has not preserved the scientist from error and has not safeguarded science from shortcomings and faults. If this had been the case, scientists would not have disagreed upon any point of science. ... It is not the person who studies the books of his predecessors and gives a free rein to his natural disposition to regard them favourably who is the real seeker after truth. But rather the person who is thinking about them is filled with doubts, who holds back with his judgement with respect to what they say, who follows proof and demonstration rather than the assertions of a man whose natural disposition is characterized by all kinds of defects and shortcomings. A person who studies scientific books with a view to knowing the truth ought to turn himself into a hostile critic of everything that he studies. ... And ... he should also be suspicious of himself ... If he takes this course, the truth will be revealed to him and the flaws in the writings of his predecessors will stand out clearly. ... " —Alhazen, (Ibn Al-Haytham) Critique of Ptolemy, translated by S. Pines, Actes X Congrès internationale d'histoire des sciences, Vol I Ithaca 1962, as referenced on p.139 of Sambursky, Shmuel (ed.) (1974), Physical Thought from the Presocratics to the Quantum Physicists, Pica Press, ISBN 0-87663-712-8{{citation}}:|first=has generic name (help)
- - perhaps retrospective claims, including criticism, and also impact, of scientific method, might be put in this proposed section.
- - perhaps this proposed section might be placed at the end of the article, just after the 'Relationship with mathematics' section. --Ancheta Wis (talk) 16:12, 24 September 2009 (UTC)
- The basic reason that diagnosis per se does not lead to scientific law is that it is part of an application of knowledge (here, medicine) and the mission of a physician/clinician is to seek a cure if possible.
- It's not the authority of the experts, it's their ability to separate what is meaningful from extraneous chaff; since they have worked in the field for so long or so extensively, what is meaningful is second nature to them. A demonstration follows:
- Science did not spring full-blown from the brow of any human being; it evolved from the needs of humanity, step by step. (I believe this is obvious, but the quotation from Alhazen below should prove it, because any controversy would not have arisen from any scientific effort, similarly to the action of angels ("If men were angels, we would have no need of government." —James Madison)), and there seems to be no lack of controversy when people congregate in large enough groups.
- Categorical statements, like that of Thales, document the beginning of the scientific impulse (meaning the desire to get at the root of things, their nature). Thales' specific hypothesis "All things rise from water" was disproven immediately by Anaximander, one of his students. This hypothesis is truly part of history of science because it was falsifiable.
- When civilizations like the Egyptians painstakingly accumulated cures for human diseases, as well as the diagnoses of diseases, as well as the prognoses for the respective diseases, this served as part of the foundation of knowledge, some of which is in use in medicine to this day.
- When subsequent civilizations, like the Greeks observed the successes and failure of their predecessors, they began to examine why. This too is part of the scientific enterprise and part of any standard history of science book.
- Once successes began to accumulate in an obvious mass, such as that evinced by Stevinus' experiment to drop weights from a height, or the rolling of balls down a ramp by Galileo, or the demonstration of the finite speed of light by Roemer, etc., then it became possible to start to categorize just what it takes to progress in science. It is not only philosophers of science, who study this, but also practicing scientists, for example, those who are experiencing a change of interest and who seek to return to their roots.
- The traditions of medicine are one thread in the tapestry leading to the rubric of science and those methods which got humankind to the successes of science. You already have SteveMcCluskey's citation. --Ancheta Wis (talk) 19:31, 21 September 2009 (UTC)
- My motivation is different; when I first edited Wikipedia, I was aided immensely by User:Jnc, an acknowledged expert in the internet who contributed to it in its early days: he was chased away by hostile treatment. Eventually the miscreant was detected and banned but the damage was done by then. Since that time I have resolved to myself that when I detect a 'person of substance' I will do my part in protecting that person from being chased away from the encyclopedia. --Ancheta Wis (talk) 21:13, 21 September 2009 (UTC)
- When googling "a method used by mathematicians, that of 'investigating from a hypothesis' " I found a commentary on Meno: Michael Cormack (2006) Plato's stepping stones: degrees of moral virtue --Ancheta Wis (talk) 01:02, 19 August 2009 (UTC)
συλλογισμὸς ἐξ ὑποθέσεως syllogism from hypothesis —Preceding unsigned comment added by 24.106.44.158 (talk) 01:31, 19 August 2009 (UTC)
- Motion has both spatial and temporal features in its description. The visual system of the brain has change-sensitive components; a saccade of the eye across a regular array of features would also be interpreted by the brain as a series of pulses, just as if one were to stimulate it with a pulse train; if one googles "tuned spatial filter" one can find some pertinent statements about vision. However this discussion is probably taking place on the wrong page. Spatial filtering was studied by television engineers like Albert Rose 60 years ago. On this page, one appears to be restricted to dealing with slices of brain being stimulated as if it were being fed images by a live eye. --Ancheta Wis (talk) 14:16, 1 August 2009 (UTC)
Now that Kenosis has explicitly placed Confirmation into Thomas Brody's 'epistemic cycle', at what stage is it? Is Confirmation at the end of a cycle, the middle, or a new beginning? Would Kuhn have called this simply part of 'normal science'?
I believe Confirmation to be akin to Victory in battle; that is, in the grander scheme, a victory simply ratifies an already existing condition in the hearts and minds of men, and a new set of forces can then arise. Or, as Kuhn puts it, a new paradigm has arisen. Just as the placement of the keystone in an arch is the last step in construction of the arch, which is then stable against collapse, so too, Confirmation is the end of a series of events; something has been settled, not just for the individual researcher who has made a discovery, but also some question has been settled in a larger community of researchers and allies who share something of the same vocabulary, definitions, processes, agreements, and allegiances. When viewed in a larger theater, a victory in battle then allows troop formations to be re-deployed, to fight again; in that sense, victory is elusive, as war in a larger theater can still be lost, and the confirmation step is but one in a larger epistemic cycle. Lastly, Confirmation is a new beginning in a larger understanding of the scheme of things.
A prototype for this is Newton's System of the World, in Book Three of Philosophiæ Naturalis Principia Mathematica. Newton's Laws have been confirmed, and the System of the World is subject to them. This was the viewpoint for two hundred years, at the end of which Einstein could ask himself 'what would the world look like if I were to ride on a beam of light?'. The answer, of course, overturned Newton's System of the World and a new world order arose, in another epistemic cycle.
In this light, I propose moving the example of the precession of the perihelion of Mercury to the Confirmation section, as signal that a new cycle, a new battle in a larger war, is looming, the end of which has not been fully determined, to this day. Although General Relativity is a victory in a smaller skirmish, it is an open question of when and how the keystone unifying relativity and quantum mechanics will be placed.
In the DNA example, which is a smaller one, compared to the unfinished structure in physics, Confirmation was the acceptance of the structure of DNA by the community of researchers. Crick and a series of other researchers could then devote their attention to the unravelling of the genetic code. In this viewpoint, the 'Transforming principle' discovered by Avery, MacLeod, and McCarty (1944) was finally accepted in the larger community of researchers, after the discovery of the structure of DNA (1953); a Nobel prize was never awarded to Avery.
To follow up on the Victory analogy, after victory in World War II, Churchill was unseated, as men could then face newer, more pressing matters than winning a war.
- Other reasons for its length are the interrelation between method and history, the fact that method is intimately tied to thinking, and the fact that scientific method is specialized for discovering new knowledge. Although it may seem that method could be further simplified or automated, and some progress has been made in this direction, the fact remains that so far, progress in science depends on talented people. It could be argued that scientific method allows for division of responsibility so that lesser-talented people can also contribute to science. However it takes insight for progress to occur in science. Lee Smolin has commented that the character of the researchers determines the direction of their results. The ambitions of Francis Crick and James Watson are exemplars of this fact. A quotation from Alhazen himself, on this page (the one that says "...God has not protected scientists from error...") shows this has been true for at least a thousand years.

- While investigating "Hebbian potentiation in Aplysia" I found "Enhancement of sensorimotor connections by conditioning-related stimulation in Aplysia depends upon postsynaptic Ca2+" which has a 14-word title, a 250 word abstract, and a six page article, freely available on the web. However, the article would take a layman weeks to understand, so this violates the 'intersubjective' requirement. The basics for 'verifiability' are simpler. Donald Hebb posited a mechanism for learning in 1949 which has served as a framework for subsequent research in neuroscience. Long term potentiation is a neurological phenomenon discovered in rabbit hippocampus; Eric Kandel realized that Aplysia, the California sea slug, which has much larger neurons, might be a better research animal than rabbits, mice, or macaques; Kandel got the 2000 Nobel prize in physiology or medicine for his work in neurobiology. As a hypothesis, LTP is thought to lie at the root of learning and memory. A host of researchers are at work on this, in multiple fields.
- The topic is not popular knowledge yet, but if it got into the article, perhaps it might become a lay topic.
- The general topic article for this is synaptic plasticity, which takes as thesis the idea that our neural dendrites undergo (reversible) physical changes when we learn.
durch planmässiges Tattonieren (through systematic palpable experimentation). —Carl Friedrich Gauss, when asked how he came about his theorems. Alan L Mackay (ed. 1991), Dictionary of Scientific Quotations London: IOP Publishing Ltd ISBN 0-7503-6106-6 Parameter error in {{ISBN}}: checksum
Perhaps more examples would better serve the article, such as mirror neurons
Giacomo Rizzolatti and Laila Craighero (2004), "The mirror-neuron system" Annual Review of Neuroscience 27: 169-192 (July 2004) doi:10.1146/annurev.neuro.27.070203.144230 Some history behind Rizzolati's discovery

One idea might be to publicize some simple (though non-obvious) observations which are reproducible, with constraints on the conditions. For example, if you are fortunate enough to have a newborn baby, during its sensitive period for this, just stick out your tongue at it, and your baby will imitate this. Older babies, children, and adults will not do this spontaneously. Human newborn babies and primate newborns have this capability in common, as shown in the image.
It is thought that mothers and fathers, while playing with their babies, have used the basis behind this phenomenon since time immemorial to teach the babies by imitation (i.e. call this hypothesis 1). Some speculate that difficulties with the mirror-neuron 'circuitry' may lie at the root of autism (call this hypothesis 1-1). As an example of scientific method in action, we have a surprising observation (the image), attendant hypotheses (1 and 1-1), predictions from the hypotheses (for example the mathematical model below), and suggested experiments (see below) to validate the concepts.
First images of a memory being formed, in Aplysia , the California sea slug.

Other examples for the article might be the hypotheses that mechanisms for synaptic plasticity of the chemical synapses lie at the root of learning and memory. There are now mathematical models for the shape of neurons' action potentials in the hippocampus, the amygdala, and other parts of the brain. There are general frameworks, such as learning based on Hebbian theory which have existed since the 1940s, and the research in neurobiology using California sea slugs has even yielded a Nobel prize for Eric Kandel. --Ancheta Wis (talk) 09:05, 12 June 2009 (UTC)
Perhaps an example from neurobiology might help the article. For example, if we were to discuss Hebb's rule as an example of a framework in molecular psychology to organize research on chemical synapses, and list some hypotheses which stem from it (such as long-term potentiation being the neural correlate of memory and learning), give some predictions (such as [http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2246410 Philip Hunter (2008) "Ancient rules of memory. The molecules and mechanisms of memory evolved long before their ‘modern' use in the brain" EMBO Rep. (2008 February); 9(2): 124–126.
doi: 10.1038/sj.embor.2008.5.]) and experimental results from work on California sea slugs, then perhaps more interest might be stimulated in the article. --Ancheta Wis (talk) 12:43, 9 June 2009 (UTC)
I propose a second extended example, from neuroscience: LTP (long-term potentiation). There is enough out there that a popular-science book on synaptic plasticity has appeared which mentions LTP, but the topic is not widespread yet thirty-five years after its discovery by T. Lomo and T. Bliss. (ref for example Tim Bliss, Graham Collingridge and Richard Morris, editors (2004) Long-term Potentiation: Enhancing Neuroscience for 30 Years ISBN 0-19-853030-7 )
N. Volfovsky, H. Parnas, M. Segal, and E. Korkotian "Geometry of Dendritic Spines Affects Calcium Dynamics in Hippocampal Neurons: Theory and Experiments " The Journal of Neurophysiology Vol. 82 No. 1 July 1999, pp. 450-462
One can view scientific method as about our limitations; cognitively, we tend to 'fill in the blanks' or 'connect the dots' when faced with gaps in our understanding. S. T. Coleridge referred to this phenomenon as the "esemplastic nature of the imagination", in which we unify our current sensations, percepts, and concepts into a seemingly seamless whole. These aspects of wholeness have been called qualia. (ref V. S. Ramachandran (1998) Phantoms in the Brain ISBN 0-965-068019 Parameter error in {{ISBN}}: checksum )
Thus we have a subject with
- 1) a known framework which has existed since the 1960s
- 2) a hypothesis that LTP is the neural correlate and the foundation of memory (and perhaps learning)
- 3) a ton of predictions with
- 4) corresponding experiments
and even better, there is controversy over whether the hypothesis is proven, as of 2008.
The subject is huge, and even Nobel laureates have been outdistanced in the race for priority.
What say you? --Ancheta Wis (talk) 12:42, 4 June 2009 (UTC)
- Jsd, your thoughts are demonstrably inaccurate.
- You mis-attribute a quote to Tetrast. If might help if you read more carefully.
- You confuse mathematical physics with theoretical physics.
- Based on this confusion, you attack.
- You criticize a classical model from 2300 years ago and Peirce's model as not part of the article, when they formed it.
- --Ancheta Wis (talk) 15:37, 3 June 2009 (UTC)
"Ditto for Acton, Numerical Methods that Work. Are these methods not methods? Is computer science not science? Why should these not count as scientific methods?" -- from Jsd
- Jsd, Thank you for showing some of your sources. In general, the limitations of an algorithm, (the Numerical Methods) need to be considered along with the problem they are attacking. CS (computer science) needs to be distinguished from engineering, which is the general domain for numerical methods. In this case, the hypothesis is that the engineering has been done before the numerical run, meaning that the numerical run will behave in an expected way. How do you know the method will not fail, without a clear statement of the limitations of the method? I guarantee you that blind reliance on algorithm will run the system, blindly, until something fails (like the current state of the global economy) and the debacle is obvious to everyone.
- In other words, for a numerical run, the researcher has to have an expectation about the answer. Otherwise the researcher is flying blind, and we are confronted with the spectacle of a man with a machine and no insight. (This is a paraphrase of Richard Hamming#Quotes)
Tambays, I was surprised to note the omission of any Philippine in the Green Man article. From my readings, for example at a UCLA art exhibit, I learned that way before the arrival of the Spanish, vegetation figures (carved of ferns etc.) were set up to scare off outsiders and to mark territory. Does anyone have additional information? --Ancheta Wis (talk) 17:56, 26 May 2009 (UTC)
I propose another example, long term potentiation (LTP); like DNA, it has a long history, with roots extending back to the nineteenth century, at least as far back as Ramón y Cajal's research. One of the advantages of presenting LTP as an example might be that LTP rests on the DNA example, and might serve as an illustration of the interconnectedness of the scientific enterprise. An LTP example could illustrate the hard work that one must perform in the service of science, such as the establishment of terminology, setting scope, understanding of technique and underlying technology (such as mouse physiology), and could also illustrate the lure of attractive analogies, such as that between LTP and long term memory. --Ancheta Wis (talk) 11:48, 20 May 2009 (UTC)
- , if 'the science is the science', meaning that the science we discover need not coincide with our previous beliefs about a subject, but that the truth which we discover is what we have to live with afterward, then this is a Pandora's box for humankind. For example, in physics, what we are learning is that the world we live in was fantastically improbable; that we live in a world far from equilibrium and that we are doomed to return to a cold, bleak nothingness, but also that we came from the heavens; that we are literally made from the stars.
- Whewell thought long and hard about method.
Here is some data about risk in computer models. Overreliance on value at risk was a factor in the global financial crisis. --Ancheta Wis (talk) 15:06, 3 March 2009 (UTC)
One concern about the operational paradigm which comes to mind is the separation of magic from science. The separation occurred in the West during the seventeenth century (p. 86, Joseph Needham, Colin A. Ronan, The Shorter Science and Civilisation in China). What is to keep some gullible government agency from funding a completely unfounded speculation, rather than funding a proposal whose prpjections are firmly grounded in scientific experiment? An administration seeking more bang for the taxpayer buck might select the proposal promising the greater projected return on investment, rather than the increase in understanding of a topic. It takes vision to make such a selection; the current state of the art in business, for example, is the spreadsheet, which takes quarterly results, finds a mathematical expression which embodies those results, and simply projects them forward. It doesn't take too much imagination to conjure up a mess, which is the state of our global economy today. What is to keep debacles in mathematical modeling from recurring, given the primitive state of the models? If a paradigm ever needed reexamination, it would be the blind use of models in place of the understanding, the comprehension of an issue. One might argue that blame for the current state of our global economy rests on the mathematical wizards who uncritically implement the mutterings of their analysts. --Ancheta Wis (talk) 14:39, 3 March 2009 (UTC)
The novel is written in crosscuts, starting with Belknap, crosscutting to Bancroft, back and forth to the climax with a pessimistic denoument. Andrea Bancroft is the daughter of a Bancroft whose divorced wife worked for the Bancroft Foundation. Andrea works for Coventry, a hedge fund; her intellect shows her to be a worthy trustee of the Bancroft Foundation, whose head is Paul Bancroft. Paul shows himself to be an attractive figure to Andrea, who plays basketball with Brandon to prove her worthiness for the trusteeship at the foundation. Unfortunately, Paul indicates he believes in the greatest good for the greatest number and has the financial strength to back his cause. Andrea is attracted to the idea, but not to its logical consequence, Theta Corporation. Theta uses a supercomputer in Research Triangle Park to calculate the number of people who would benefit when a key person is terminated. Paul must approve these actions to increase the greatest good.
Brandon is Paul's son and intellectual equal. Unbeknown to anyone until the climax, Brandon is attempting to destroy Theta with an internet presence, Genesis.
Mike Garrison retrieves Belknap's security clearance, forcing Belknap to go it alone. Belknap asks a friend to bug Andrea's house, who discovers the house is already bugged, and is assassinated himself. Belknap asks help from another CIA operative to tell him about Genesis; during the meeting, his CIA friend is killed by a sniper.
Belknap is travelling the world to discover who has captured Pollux, who is his only constant friend, having lost his wife and girlfriends to spy operations. Belknap discovers he is on a list of assassinated people, after he has killed several hit squads, and that there is a link to Theta.
Castor tracks down a Genesis candidate and discovers that Lugner has been hiding in Estonia; this makes Pollux, Castor's only supposed friend, a fraud. Andrea, in the meantime, has run into Bancroft (Castor) and is attempting to flee to him after being forced to kill two employees of Theta in the records section of Iron Mountain, to save herself, for the first time. Andrea is drugged and rescued by Belknap where they return to the US.
- I have never seen a solution except for the Globe in the upper left hand corner of this page, probably hard-coded to get to the Main page. If anyone solves this problem, it will have an enormous effect for good on the encyclopedia. --Ancheta Wis (talk) 14:13, 25 January 2009 (UTC)
I was going to add the Crab Supernova of 1054 as an example of observer bias, because Britannica notes that no European scientific records of the supernova exist, although Chinese, Japanese, Arab and possibly Native American astronomers record the event. In fact, the star was visible during the day. How could this be? That's when I got discouraged about entering it in the article, because of OR concerns. One plausible explanation is that when the Crab Supernova was visible, it appeared in the celestial sphere of the Moon, which was supposed to be perfect in the European mythology, as opposed to the imperfect terrestial sphere which man inhabits. Thus comets must be in the terrestial sphere as they are harbingers of evil, etc. But if the Crab Supernova was in the sphere of the Moon, that was impossible. Q.E.D.
I agree that this makes no sense. And I don't have a citation for this example of bias. --Ancheta Wis (talk) 03:54, 4 January 2009 (UTC)
- Citations are definitely in order here. It is unfortunate that the literature of the ipl site you list above refers to concepts which have little credibility in our current time. If you look at the theory of the Chinese seismometer from 124 CE, it refers to dragons etc. We have been trained to disregard those concepts and some bridge articles to translate them to more palatable terms are probably in order. When Newton framed the mechanistic view of the world he moved world civilization away from the unobservables, while still keeping the work of the Ancients, such as Apollonius, Archimedes, etc. Their work survives in the current edifice called Science. But not dragons. What the article needs is concrete advances, their citations, and perhaps some sub-articles. But there is a difference between technology and science. The Four Great Inventions are technology. If you want a starting point, Thales' speculation on the nature of matter is considered by some to be the beginning of science. Now I am not an expert on the corresponding Chinese literature, but where are the citations for the analog of Thales? I am aware that air or chi is very important to Chinese civilization, to the extent that a mother will blow on a child's hurt to soothe it, but where is the literature that speaks to the phases of air, in a similar way as Thales' phases of water? --Ancheta Wis (talk) 21:28, 22 December 2008 (UTC)
- And yet, we are still subject to free-fall (motion along the geodesic) when Earth looses its grip on us. It is possible to experience this on Earth's surface,
- for example on a seashore, standing in the surf, as a wave crashes over our legs; we stand on the sand, upright, while the ocean rips away the sand beneath us; we fall through the sand, sinking toward Earth's center, until our feet arrive at sand which remains under the grip of gravitation, and which has not yet moved due to the ocean wave. As the ocean wave recedes, our formerly free feet are now buried in sand. But can you imagine, if more sand had been washed away, beneath our feet, we would have fallen even further during our descent through the sand! If you want to reproduce this, try a barrier island such as Cape Hatteras, North Carolina and just walk through the surf. The sand there is loose enough to be easily subject to the waves of the Atlantic Ocean, irrespective of Man's attempts to stabilize what are basically sand dunes in the ocean.
- Other well-known examples of the result of inertial motion are the feeling we get as an elevator starts its downward motion and
- The feeling we first get during an earthquake, when Earth suddenly moves down with respect to the former surface. We are so used to Earth's gravity that we do not realize that we sense it all the time with the organs of balance in our body. This is an aspect of the sense of proprioception, part of the somatosensory system.
- And yet, we are still subject to free-fall (motion along the geodesic) when Earth looses its grip on us. It is possible to experience this on Earth's surface,
- This exchange of views between editors has actually clarified in my mind what we term inertial coordinates:
- we first isolate the part of the system which is in inertial motion
- we compare to the part of the system which is subject to other forces (we write down the geometry of the respective parts of the system, inertial versus non-inertial)
- we write down the forces (ala D'Alembert's principle)
- we solve the motion
{{RFPP|full|1 week|<reason>}} Inward Bound: Of matter and forces in the physical world ISBN 0-19-851971-0
| Name | First operational | Numeral system | Computing mechanism | Programming | Turing complete |
|---|---|---|---|---|---|
| Zuse Z3 (Germany) | May 1941 | Binary | Electro-mechanical | Program-controlled by punched film stock | Yes (1998) |
| Atanasoff–Berry Computer (US) | Summer 1941 | Binary | Electronic | Not programmable—single purpose | No |
- ^ According to the law of the diocese, Sanches would have been baptized with 9 days of his birth. Sanches, Limbrick & Thomson 1988, pp. 4–5
- ^ Francisco Sanches (ca 1551-1623) Filósofo, matemático e médico - Biblioteca Nacional de Portugal (in Portuguese)
- ^ See, for example,Horowitz & Hill 1989, pp. 1–44
- ^ Norden
- ^ Singer 1946
- ^ Phillips
- ^ (in French)Coriolis 1836, pp. 5–9
- ^ The noise level, compared to the signal level, is a fundamental factor, see for example Davenport & Root 1958, pp. 112–364.
- ^ Ziemer, Tranter & Fannin 1993, p. 370.
- ^ The publication of Two New Sciences by the House of Elzevir in Leiden, the Netherlands, could ignore any censure by the Index Librorum Prohibitorum which was only disestablished in 1966. See: Andrew Dickson White (1896), A History of the Warfare of Science with Theology in Christendom
- ^ Rod Burstall, "Christopher Strachey—Understanding Programming Languages", Higher-Order and Symbolic Computation 13:52 (2000)
- ^ See the hypothethico-deductive method, for example, Godfrey-Smith 2003, p. 236.
- ^ Jevons 1874, pp. 265–6.
- ^ pp.65,73,92,398 —Andrew J. Galambos, Sic Itur ad Astra ISBN 0-88078-004-5(AJG learned scientific method from Felix Ehrenhaft)
- ^ Galilei 1638, pp. v–xii, 1–300
- ^ Brody 1993, pp. 10–24 calls this the "epistemic cycle": "The epistemic cycle starts from an initial model; iterations of the cycle then improve the model until an adequate fit is achieved.".
- ^ Iteration example: Chaldean astronomers such as Kidinnu compiled astronomical data. Hipparchus was to use this data to calculate the precession of the Earth's axis. Fifteen hundred years after Kiddinu, Al-Batani, born in what is now Turkey, would use the collected data and improve Hipparchus' value for the precession of the Earth's axis. Al-Batani's value, 54.5 arc-seconds per year, compares well to the current value of 49.8 arc-seconds per year (26,000 years for Earth's axis to round the circle of nutation).
- ^ Recursion example: the Earth is itself a magnet, with its own North and South Poles William Gilbert (in Latin 1600) De Magnete, or On Magnetism and Magnetic Bodies. Translated from Latin to English, selection by Moulton & Schifferes 1960, pp. 113–117.
- ^ "The foundation of general physics ... is experience. These ... everyday experiences we do not discover without deliberately directing our attention to them. Collecting information about these is observation." —Hans Christian Ørsted("First Introduction to General Physics" ¶13, part of a series of public lectures at the University of Copenhagen. Copenhagen 1811, in Danish, printed by Johan Frederik Schulz. In Kirstine Meyer's 1920 edition of Ørsted's works, vol.III pp. 151-190. ) "First Introduction to Physics: the Spirit, Meaning, and Goal of Natural Science". Reprinted in German in 1822, Schweigger's Journal für Chemie und Physik 36, pp.458-488, as translated in Ørsted 1997, p. 292
- ^ "When it is not clear under which law of nature an effect or class of effect belongs, we try to fill this gap by means of a guess. Such guesses have been given the name conjectures or hypotheses." —Hans Christian Ørsted(1811) "First Introduction to General Physics" as translated in Ørsted 1997, p. 297.
- ^ "In general we look for a new law by the following process. First we guess it. ...", —Feynman 1965, p. 156
- ^ "... the statement of a law - A depends on B - always transcends experience." —Born 1949, p. 6
- ^ "The student of nature ... regards as his property the experiences which the mathematican can only borrow. This is why he deduces theorems directly from the nature of an effect while the mathematician only arrives at them circuitously." —Hans Christian Ørsted(1811) "First Introduction to General Physics" ¶17. as translated in Ørsted 1997, p. 297.
- ^ Salviati speaks: "I greatly doubt that Aristotle ever tested by experiment whether it be true that two stones, one weighing ten times as much as the other, if allowed to fall, at the same instant, from a height of, say, 100 cubits, would so differ in speed that when the heavier had reached the ground, the other would not have fallen more than 10 cubits." Two New Sciences (1638) —Galilei 1638, pp. 61–62. A more extended quotation is referenced by Moulton & Schifferes 1960, pp. 80–81.
| Articles about |
| Electromagnetism |
|---|
 |
Electromagnetism is the physics of the electromagnetic field: a field which exerts a force on particles that possess the property of electric charge, and is in turn affected by the presence and motion of those particles.
A changing magnetic field produces an electric field (this is the phenomenon of electromagnetic induction, the basis of operation for electrical generators, induction motors, and transformers). Similarly, a changing electric field generates a magnetic field. Because of this interdependence of the electric and magnetic fields, it makes sense to consider them as a single coherent entity - the electromagnetic field.
The magnetic field is produced by the motion of electric charges, i.e., electric current. The magnetic field causes the magnetic force associated with magnets.
The theoretical implications of electromagnetism led to the development of special relativity by Albert Einstein in 1905.
Overview[edit]

Electromagnetism describes the interaction of charged particles with electric and magnetic fields. It can be divided into electrostatics, the study of interactions between charges at rest, and electrodynamics, the study of interactions between moving charges and radiation. The classical theory of electromagnetism is based on the Lorentz force law and Maxwell's equations.
Electrostatics is the study of phenomena associated with charged bodies at rest. As described by Coulomb’s law, such bodies exert forces on each other. Their behavior can be analyzed in terms of the concept of an electric field surrounding any charged body, such that another charged body placed within the field is subject to a force proportional to the magnitude of its own charge and the magnitude of the field at its location. Whether the force is attractive or repulsive depends on the polarity of the charge. Electrostatics has many applications, ranging from the analysis of phenomena such as thunderstorms to the study of the behavior of electron tubes.
Electrodynamics is the study of phenomena associated with charged bodies in motion and varying electric and magnetic fields. Since a moving charge produces a magnetic field, electrodynamics is concerned with effects such as magnetism, electromagnetic radiation, and electromagnetic induction, including such practical applications as the electric generator and the electric motor. This area of electrodynamics, known as classical electrodynamics, was first systematically explained by James Clerk Maxwell, and Maxwell’s equations describe the phenomena of this area with great generality. A more recent development is quantum electrodynamics, which incorporates the laws of quantum theory in order to explain the interaction of electromagnetic radiation with matter. Paul Dirac, Werner Heisenberg, and Wolfgang Pauli were pioneers in the formulation of quantum electrodynamics. Relativistic electrodynamics accounts for relativistic corrections to the motions of charged particles when their speeds approach the speed of light. It applies to phenomena involved with particle accelerators and electron tubes carrying high voltages and currents.
Electromagnetism encompasses various real-world electromagnetic phenomena. For example, light is an oscillating electromagnetic field that is radiated from accelerating charged particles. Aside from gravity, most of the forces in everyday experience are ultimately a result of electromagnetism.
The principles of electromagnetism find applications in various allied disciplines such as microwaves, antennas, electric machines, satellite communications, bioelectromagnetics, plasmas, nuclear research, fiber optics, electromagnetic interference and compatibility, electromechanical energy conversion, radar meteorology, and remote sensing. Electromagnetic devices include transformers, electric relays, radio/TV, telephones, electric motors, transmission lines, waveguides, optical fibers, and lasers.
History[edit]
While preparing for an evening lecture on 21 April 1820, Hans Christian Ørsted developed an experiment which provided evidence that surprised him. As he was setting up his materials, he noticed a compass needle deflected from magnetic north when the electric current from the battery he was using was switched on and off. This deflection convinced him that magnetic fields radiate from all sides of a wire carrying an electric current, just as light and heat do, and that it confirmed a direct relationship between electricity and magnetism.
At the time of discovery, Ørsted did not suggest any satisfactory explanation of the phenomenon, nor did he try to represent the phenomenon in a mathematical framework. However, three months later he began more intensive investigations. Soon thereafter he published his findings, proving that an electric current produces a magnetic field as it flows through a wire. The CGS unit of magnetic induction (oersted) is named in honor of his contributions to the field of electromagnetism.
His findings resulted in intensive research throughout the scientific community in electrodynamics. They influenced French physicist André-Marie Ampère's developments of a single mathematical form to represent the magnetic forces between current-carrying conductors. Ørsted's discovery also represented a major step toward a unified concept of energy.
Ørsted was not the first person to examine the relation between electricity and magnetism. In 1802 Gian Domenico Romagnosi, an Italian legal scholar, deflected a magnetic needle by electrostatic charges. He interpreted his observations as The Relation between electricity and magnetism. Actually, no galvanic current existed in the setup and hence no electromagnetism was present. An account of the discovery was published in 1802 in an Italian newspaper, but it was largely overlooked by the contemporary scientific community.
This unification, which was observed by Michael Faraday, extended by James Clerk Maxwell, and partially reformulated by Oliver Heaviside and Heinrich Hertz, is one of the accomplishments of 19th century mathematical physics. It had far-reaching consequences, one of which was the understanding of the nature of light. As it turns out, what is thought of as "light" is actually a propagating oscillatory disturbance in the electromagnetic field, i.e., an electromagnetic wave. Different frequencies of oscillation give rise to the different forms of electromagnetic radiation, from radio waves at the lowest frequencies, to visible light at intermediate frequencies, to gamma rays at the highest frequencies.
The electromagnetic force[edit]
The force that the electromagnetic field exerts on electrically charged particles, called the electromagnetic force, is one of the fundamental forces, and is responsible for most of the forces we experience in our daily lives. The other fundamental forces are the strong nuclear force (which holds atomic nuclei together), the weak nuclear force and the gravitational force. All other forces are ultimately derived from these fundamental forces.
The electromagnetic force is the one responsible for practically all the phenomena encountered in daily life, with the exception of gravity. All the forces involved in interactions between atoms can be traced to the electromagnetic force acting on the electrically charged protons and electrons inside the atoms. This includes the forces we experience in "pushing" or "pulling" ordinary material objects, which come from the intermolecular forces between the individual molecules in our bodies and those in the objects. It also includes all forms of chemical phenomena, which arise from interactions between electron orbitals.
Classical electrodynamics[edit]
The scientist William Gilbert proposed, in his De Magnete (1600), that electricity and magnetism, while both capable of causing attraction and repulsion of objects, were distinct effects. Mariners had noticed that lightning strikes had the ability to disturb a compass needle, but the link between lightning and electricity was not confirmed until Benjamin Franklin's proposed experiments in 1752. One of the first to discover and publish a link between man-made electric current and magnetism was Romagnosi, who in 1802 noticed that connecting a wire across a voltaic pile deflected a nearby compass needle. However, the effect did not become widely known until 1820, when Ørsted performed a similar experiment. Ørsted's work influenced Ampère to produce a theory of electromagnetism that set the subject on a mathematical foundation.
An accurate theory of electromagnetism, known as classical electromagnetism, was developed by various physicists over the course of the 19th century, culminating in the work of James Clerk Maxwell, who unified the preceding developments into a single theory and discovered the electromagnetic nature of light. In classical electromagnetism, the electromagnetic field obeys a set of equations known as Maxwell's equations, and the electromagnetic force is given by the Lorentz force law.
One of the peculiarities of classical electromagnetism is that it is difficult to reconcile with classical mechanics, but it is compatible with special relativity. According to Maxwell's equations, the speed of light in a vacuum is a universal constant, dependent only on the electrical permittivity and magnetic permeability of free space. This violates Galilean invariance, a long-standing cornerstone of classical mechanics. One way to reconcile the two theories is to assume the existence of a luminiferous aether through which the light propagates. However, subsequent experimental efforts failed to detect the presence of the aether. After important contributions of Hendrik Lorentz and Henri Poincaré, in 1905, Albert Einstein solved the problem with the introduction of special relativity, which replaces classical kinematics with a new theory of kinematics that is compatible with classical electromagnetism. (For more information, see History of special relativity.)
In addition, relativity theory shows that in moving frames of reference a magnetic field transforms to a field with a nonzero electric component and vice versa; thus firmly showing that they are two sides of the same coin, and thus the term "electromagnetism". (For more information, see Classical electromagnetism and special relativity.)
The photoelectric effect[edit]
In another paper published in that same year, Albert Einstein undermined the very foundations of classical electromagnetism. His theory of the photoelectric effect (for which he won the Nobel prize for physics) posited that light could exist in discrete particle-like quantities, which later came to be known as photons. Einstein's theory of the photoelectric effect extended the insights that appeared in the solution of the ultraviolet catastrophe presented by Max Planck in 1900. In his work, Planck showed that hot objects emit electromagnetic radiation in discrete packets, which leads to a finite total energy emitted as black body radiation. Both of these results were in direct contradiction with the classical view of light as a continuous wave. Planck's and Einstein's theories were progenitors of quantum mechanics, which, when formulated in 1925, necessitated the invention of a quantum theory of electromagnetism. This theory, completed in the 1940s, is known as quantum electrodynamics (or "QED"), and is one of the most accurate theories known to physics.
Definition[edit]
The term electrodynamics is sometimes used to refer to the combination of electromagnetism with mechanics, and deals with the effects of the electromagnetic field on the dynamic behavior of electrically charged particles.
Units[edit]
Electromagnetic units are part of a system of electrical units based primarily upon the magnetic properties of electric currents, the fundamental cgs unit being the ampere. The units are:
In the electromagnetic cgs system, electrical current is a fundamental quantity defined via Ampère's law and takes the permeability as a dimensionless quantity (relative permeability) whose value in a vacuum is unity. As a consequence, the square of the speed of light appears explicitly in some of the equations interrelating quantities in this system.
| Symbol[1] | Name of Quantity | Derived Units | Unit | Base Units |
|---|---|---|---|---|
| I | Electric current | ampere (SI base unit) | A | A (= W/V = C/s) |
| Q | Electric charge | coulomb | C | A·s |
| U, ΔV, Δφ; E | Potential difference; Electromotive force | volt | V | J/C = kg·m2·s−3·A−1 |
| R; Z; X | Electric resistance; Impedance; Reactance | ohm | Ω | V/A = kg·m2·s−3·A−2 |
| ρ | Resistivity | ohm metre | Ω·m | kg·m3·s−3·A−2 |
| P | Electric power | watt | W | V·A = kg·m2·s−3 |
| C | Capacitance | farad | F | C/V = kg−1·m−2·A2·s4 |
| E | Electric field strength | volt per metre | V/m | N/C = kg·m·A−1·s−3 |
| D | Electric displacement field | coulomb per square metre | C/m2 | A·s·m−2 |
| ε | Permittivity | farad per metre | F/m | kg−1·m−3·A2·s4 |
| χe | Electric susceptibility | (dimensionless) | - | - |
| G; Y; B | Conductance; Admittance; Susceptance | siemens | S | Ω−1 = kg−1·m−2·s3·A2 |
| κ, γ, σ | Conductivity | siemens per metre | S/m | kg−1·m−3·s3·A2 |
| B | Magnetic flux density, Magnetic induction | tesla | T | Wb/m2 = kg·s−2·A−1 = N·A−1·m−1 |
| Φ | Magnetic flux | weber | Wb | V·s = kg·m2·s−2·A−1 |
| H | Magnetic field strength | ampere per metre | A/m | A·m−1 |
| L, M | Inductance | henry | H | Wb/A = V·s/A = kg·m2·s−2·A−2 |
| μ | Permeability | henry per metre | H/m | kg·m·s−2·A−2 |
| χ | Magnetic susceptibility | (dimensionless) | - | - |
Electromagnetic phenomena[edit]
| This user page may require cleanup to meet Wikipedia's quality standards. No cleanup reason has been specified. Please help improve this user page if you can. |
In the theory, electromagnetism is the basis for optical phenomena, as discovered by James Clerk Maxwell while he studied electromagnetic waves.[2] Light, being an electromagnetic wave, has properties that can be explained through Maxwell's equations, such as reflection, refraction, diffraction, interference and others. Relativity is born on the electromagnetic fields, as shown by Albert Einstein when he tried to make the electromagnetic theory compatible with Planck's radiation formula.[3]
See also[edit]
References[edit]
This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. (February 2008) |
- ^ International Union of Pure and Applied Chemistry (1993). Quantities, Units and Symbols in Physical Chemistry, 2nd edition, Oxford: Blackwell Science. ISBN 0-632-03583-8. pp. 14–15. Electronic version.
- ^ The Light Cone: Maxwell and the Electrodynamic Theory of Light
- ^ On Einstein's distrust of the electromagnetic theory: The origin of the light-velocity postulate
Web
- Nave, R., Magnetic Field Strength H, retrieved 2007-06-04
- Keitch, Paul, Magnetic Field Strength and Magnetic Flux Density, retrieved 2007-06-04
- Oppelt, Arnulf (2006-11-02), magnetic field strength, retrieved 2007-06-04
{{citation}}: Check date values in:|date=(help) - magnetic field strength converter, retrieved 2007-06-04
Books
- Durney, Carl H. and Johnson, Curtis C. (1969). Introduction to modern electromagnetics. McGraw-Hill. ISBN 0-07-018388-0.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Rao, Nannapaneni N. (1994). Elements of engineering electromagnetics (4th ed.). Prentice Hall. ISBN 0-13-948746-8.
- Tipler, Paul (1998). Physics for Scientists and Engineers: Vol. 2: Light, Electricity and Magnetism (4th ed. ed.). W. H. Freeman. ISBN 1-57259-492-6.
{{cite book}}:|edition=has extra text (help) - Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed. ed.). Prentice Hall. ISBN 0-13-805326-X.
{{cite book}}:|edition=has extra text (help) - Jackson, John D. (1998). Classical Electrodynamics (3rd ed. ed.). Wiley. ISBN 0-471-30932-X.
{{cite book}}:|edition=has extra text (help) - Rothwell, Edward J. (2001). Electromagnetics. CRC Press. ISBN 0-8493-1397-X.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Wangsness, Roald K. (1986). Electromagnetic Fields (2nd Edition). Wiley. ISBN 0-471-81186-6.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Dibner, Bern (1961). Oersted and the discovery of electromagnetism. Blaisdell Publishing Company. ISSN 99-0317066-1 ; 18.
External links[edit]
- Mag Lab U: Lessons on Electricity and Magnetism National High Magnetic Field Laboratory
- Circuit Construction Kit PhET at University of Colorado, Boulder
- Electromagnetic Tutorials and Forums EM Talk
- ışık
- MIT Video Lectures - Electricity and Magnetism from Spring 2002. Taught by Professor Walter Lewin.
- Electricity and Magnetism - an online textbook (uses algebra, with optional calculus-based sections)
- Electromagnetic Field Theory - an online textbook (uses calculus)
- Classical Electromagnetism: An intermediate level course - an online intermediate level texbook downloadable as PDF file
- Science Aid: electromagnetism Electromagnetism, aimed at teens.
- Motion Mountain A modern introduction to electromagnetism and its effects in everyday life.
- Books on Electromagnetism and RF field
- Gallery of Electromagnetic Personalities
- MSci Electromagnetic Theory Lecture Notes
- PHY2206 Electromagnetic Fields Course Handouts
- Dr. David Kagan Physics 204B Lecture Notes
- Sophocles J. Orfanidis' Electromagnetic Waves and Antennas
- MAS207 Electromagnetism Lecture Notes
- PHYS1002 - Electromagnetism, Optics, Relativity and Quantum Physics I
- Dr. Zbigniew Ficek's PHYS3050 Electromagnetic theory lecture notes
- Elektromanyetik kuvvet
- University of Cambridge's Advanced Physics Electromagnetism
- ECEN4364 Principles of RF and Microwave Measurements lecture notes
- B7 Relativity and Electromagnetism
- NMJ Woodhouse's Special Relativity and Electromagnetism
- NMJ Woodhouse's General Relativity
- Maxwell, Mechanism and the Nature of Electricity
- Electromagnetism Mathematica notes
- "National Grid", electromagnetic sound art
- "Disinformation", electromagnetic sound art
- Differential Forms in Electromagnetic Theory
- The Life of James Clerk Maxwell - prepared by James C. Rautio of Sonnet Software, Inc.
- Classical Electrodynamics and Theory of Relativity - by Ruslan Sharipov
- Axial Vectors - by Alain Bossavit
- research of electromagnetics used to predict earthquakes: http://www.quakefinder.com/research/em_sources.php
Mechanics (Greek Μηχανική) is the branch of physics concerned with the behaviour of physical bodies when subjected to forces or displacements, and the subsequent effect of the bodies on their environment. The discipline has its roots in several ancient civilizations (see History of classical mechanics and Timeline of classical mechanics). During the early modern period, scientists such as Galileo, Kepler, and especially Newton, laid the foundation for what is now known as classical mechanics.

Classical mechanics[edit]
Classical mechanics is a model of the physics of forces acting upon bodies. It is often referred to as "Newtonian mechanics" after Isaac Newton and his laws of motion. Mechanics is subdivided into statics, which models objects at rest, kinematics, which models objects in motion, and dynamics, which models objects subjected to forces. The classical mechanics of continuous and deformable objects is continuum mechanics, which can itself be broken down into solid mechanics and fluid mechanics according to the state of matter being studied. The latter, the mechanics of liquids and gases, includes hydrostatics, hydrodynamics, pneumatics, aerodynamics, and other fields. Mechanical Statics deals with objects at rest. Mechanical kinematics deals with objects in motion. Mechanical dynamics deals with motion of objects subject to forces.
Classical mechanics produces accurate results within the domain of everyday experience. It is superseded by relativistic mechanics for systems moving at large velocities near the speed of light, quantum mechanics for systems at small distance scales, and relativistic quantum field theory for systems with both properties. Nevertheless, classical mechanics is still useful, because it is much simpler and easier to apply than these other theories, and it has a very large range of approximate validity. Classical mechanics can be used to describe the motion of human-sized objects (such as tops and baseballs), many astronomical objects (such as planets and galaxies), and certain microscopic objects (such as organic molecules).
An important concept of mechanics is the identification of conserved energy and momentum, which lead to the Lagrangian and Hamiltonian reformulations of Newton's laws. Theories such as fluid mechanics and the kinetic theory of gases result from applying classical mechanics to macroscopic systems. A relatively recent result of considerations concerning the dynamics of nonlinear systems is chaos theory, the study of systems in which small changes in a variable may have large effects. Newton's law of universal gravitation, formulated within classical mechanics, explained Kepler's laws of planetary motion and helped make classical mechanics an important element of the Scientific Revolution.
Classical versus quantum[edit]
| Part of a series on |
| Classical mechanics |
|---|
| Part of a series of articles about |
| Quantum mechanics |
|---|
The major division of the mechanics discipline separates classical mechanics from quantum mechanics.
Historically, classical mechanics came first, while quantum mechanics is a comparatively recent invention. Classical mechanics originated with Isaac Newton's Laws of motion in Principia Mathematica, while quantum mechanics didn't appear until 1900. Both are commonly held to constitute the most certain knowledge that exists about physical nature. Classical mechanics has especially often been viewed as a model for other so-called exact sciences. Essential in this respect is the relentless use of mathematics in theories, as well as the decisive role played by experiment in generating and testing them.
Quantum mechanics is of a wider scope, as it encompasses classical mechanics as a sub-discipline which applies under certain restricted circumstances. According to the correspondence principle, there is no contradiction or conflict between the two subjects, each simply pertains to specific situations. Quantum mechanics has superseded classical mechanics at foundational level and is indispensable for the explanation and prediction of processes at molecular and (sub)atomic level. However, for macroscopical processes classical mechanics is able to solve problems which are unmanageably difficult in quantum mechanics and hence remains useful and well used.
Einsteinian versus Newtonian[edit]
Analogous to the quantum versus classical reformation, Einstein's general and special theories of relativity have expanded the scope of mechanics beyond the mechanics of Newton and Galileo, and made fundamental corrections to them, that become significant and even dominant as speeds of material objects approach the speed of light, which cannot be exceeded. Relativistic corrections are also needed for quantum mechanics, although relativity has not been fully integrated with it yet; this is one of the hurdles that has to be overcome in developing a Grand Unified Theory.
Types of mechanical bodies[edit]
Thus the often-used term body needs to stand for a wide assortment of objects, including particles, projectiles, spacecraft, stars, parts of machinery, parts of solids, parts of fluids (gases and liquids), etc.
Other distinctions between the various sub-disciplines of mechanics, concern the nature of the bodies being described. Particles are bodies with little (known) internal structure, treated as mathematical points in classical mechanics. Rigid bodies have size and shape, but retain a simplicity close to that of the particle, adding just a few so-called degrees of freedom, such as orientation in space.
Otherwise, bodies may be semi-rigid, i.e. elastic, or non-rigid, i.e. fluid. These subjects have both classical and quantum divisions of study.
For instance: The motion of a spacecraft, regarding its orbit and attitude (rotation), is described by the relativistic theory of classical mechanics. While analogous motions of an atomic nucleus are described by quantum mechanics.
Sub-disciplines in mechanics[edit]
The following are two lists of various subjects that are studied in mechanics.
Note that there is also the "theory of fields" which constitutes a separate discipline in physics, formally treated as distinct from mechanics, whether classical fields or quantum fields. But in actual practice, subjects belonging to mechanics and fields are closely interwoven. Thus, for instance, forces that act on particles are frequently derived from fields (electromagnetic or gravitational), and particles generate fields by acting as sources. In fact, in quantum mechanics, particles themselves are fields, as described theoretically by the wave function.
Classical mechanics[edit]
The following are described as forming Classical mechanics:
- Newtonian mechanics, the original theory of motion (kinematics) and forces (dynamics)
- Lagrangian mechanics, a theoretical formalism, based on the principle of conservation of energy
- Hamiltonian mechanics, another theoretical formalism, based on the principle of the least action
- Celestial mechanics, the motion of heavenly bodies: planets, comets, stars, galaxies, etc.
- Astrodynamics, spacecraft navigation, etc.
- Solid mechanics, elasticity, the properties of (semi-)rigid bodies
- Acoustics, sound ( = density variation propagation) in solids, fluids and gases.
- Statics, semi-rigid bodies in mechanical equilibrium
- Fluid mechanics, the motion of fluids
- Soil mechanics, mechanical behavior of soils
- Continuum mechanics, mechanics of continua (both solid and fluid)
- Hydraulics, mechanical properties of liquids
- Fluid statics, liquids in equilibrium
- Applied / Engineering mechanics
- Biomechanics, solids, fluids, etc. in biology
- Biophysics, physical processes in living organisms
- Statistical mechanics, assemblies of particles too large to be described in a deterministic way
- Relativistic or Einsteinian mechanics, universal gravitation
Quantum mechanics[edit]
The following are categorized as being part of Quantum mechanics:
- Particle physics, the motion, structure, and reactions of particles
- Nuclear physics, the motion, structure, and reactions of nuclei
- Condensed matter physics, quantum gases, solids, liquids, etc.
- Quantum statistical mechanics, large assemblies of particles
Professional organizations[edit]
- Applied Mechanics Division, American Society of Mechanical Engineers
- Fluid Dynamics Division, American Physical Society
- Institution of Mechanical Engineers is the United Kingdom's qualifying body for Mechanical Engineers and has been the home of Mechanical Engineers for over 150 years.
See also[edit]
External links[edit]
- iMechanica: the web of mechanics and mechanicians
- Mechanics Blog by a Purdue University Professor
- The Mechanics program at Virginia Tech
- Physclips: Mechanics with animations and video clips from the University of New South Wales
- U.S. National Committee on Theoretical and Applied Mechanics
Just as warfare seeks to hold the high ground, so too do competitors seek control of sources: all sorts of resources, including information. From a layman's point of view, the seemingly random creation and deletion of text on the article page seems arcane and pointless, until one considers the rationale for such actions. It is not enough to moot plausible motives. What is necessary is to provide citations with publicly available keys to information. For example, it is unacceptable for the encyclopedia to mark some reference with a security classification when that information is publicly available. If the information was ever publicly available, then in principle that reference is citable for the encyclopedia. Thus citations including author, date, and publication information for the referenced content serve as a package which is acceptable to the encyclopedia.
To control the battle for sources, I propose that changes to the article page be vetted on the talk page; this policy works well on other articles and takes the disputes to another level. What this does entail, is that consensus be achieved. This has the effect of stabilizing the drive-by edits. If this means that editors will need to gain some sort of reputation or currency to improve this page, then this works toward the good of the encyclopedia.
People, what say you?
- Dzybak, I see that you are interested in understanding by AI. Ludwig Wittgenstein did some work in this field about 85 years ago. See here for an example. The English language uses infix notation in much the same way you were mapping subject verb object, thus allowing English speakers to read some logic productions as if they were English sentences. And indeed this gives rise to mechanically generated ontologies. But Wittgenstein unearthed some moral dilemmas which he writes about in Tractatus_Logico-Philosophicus, the only philosophical book he published in his lifetime. I alluded to them in the paragraph above. --Ancheta Wis (talk) 11:56, 21 July 2008 (UTC)
- Welcome to wikipedia. If you have content to contribute to the article, or a comment about the article, then Be Bold. I have a personal preference for subjunctive mood, so I would have written 'If there were a technique', which puts the reader in the mood for hypotheticals. I also have a personal preference for individual experience, and logical propositions need to be grounded, in my book. Thus the natural philosopher has an advantage over the logician, based on greater intimacy with the problem of interest. In that case, we need only to worry about the rhetoric of science, since the thinking (logic) would be correct. But if one requires proof, then,
- To address the why, it is a bit forward to state things from the point of view of today when the article clearly shows that usage has evolved in the past 50 years. In other words, an article which covers 2000 years would do well to consider how usage of an easy word like computer has shifted in meaning, much less a hard word/concept like software. Granted, hardware is the easy part, as it refers to something a bit more tangible. For example computer is misnamed. It should be called controller, if one were to be logical about it. But that's how usage has evolved, and history depends on the previous state, so computer it is.
- It is documented in Two New Sciences that Aristotle did not perform at least one of the experiments he described. Since Al-Biruni is documented to have performed experiments, and since Alhacen performed a dissection of the human visual system 500 years before Vesalius (1543), who else relied on experimentation? Only a few names survive from this period. But the writings of the authors we do know about are concrete evidence that experimentation was undertaken. --Ancheta Wis (talk) 17:52, 21 June 2008 (UTC)
I have absolutely no idea about what ancheta is talking about. What am objecting to is that the whole idea of experiment is of philisophical in nature and there is no clear consensus when it emerged and what it consititues, and is matter of debate among philosophers of physics to this day, and how it can be refined along with the scientific method. Secondly, the quotation that is used doesnt support the claim being made. Lastly, in order to make such bold claims requires several respectable sources on the topic not a book islamic science. Tomasz Prochownik (talk) 15:25, 20 June 2008 (UTC)
- I must point out that the comment about Islamic Science merely documents your bias. Only 1000 years ago Basra, Iraq was the center of scientific research on the planet. Denise Schmandt-Besserat teaches us that writing and numbers were invented in Iraq, 9000 BCE to 5000 BCE, at an earlier time that we can document, than anywhere else on the planet. In another 1000 years we humans (or our assigns) may be reading a translation of these sentences but thinking in a language completely unrelated to English.
- It would be very useful to have some standard reference on the history of physics to guide us. I don't know of one off-hand. Gnixon (talk) 15:55, 20 June 2008 (UTC)
- According to my 1989 edition of Propaedia we are in a documentation hole regarding the history of physics between Aristotle and the Scientific Revolution. Propaedia (1989) skips right from Aristotle to Western science, this is understandable because Propaedia is a Western work. But this is where Al-Biruni and Alhacen fit in the picture, because they were trying to introduce neo-Aristotelian thought into the writings of the period, as documented by the writings of the period. So Western science owes a debt to them, acknowledged or not. --Ancheta Wis (talk) 17:52, 21 June 2008 (UTC)
First-generation von Neumann machine and the other works[edit]
Even before the ENIAC was finished, Eckert and Mauchly recognized its limitations and started the design of a stored-program computer, EDVAC. John von Neumann was credited with a widely-circulated report describing the EDVAC design in which both the programs and working data were stored in a single, unified store. This basic design, denoted the von Neumann architecture, would serve as the foundation for the continued development of ENIAC's successors.[1]
In this generation, temporary or working storage was provided by acoustic delay lines, which used the propagation time of sound through a medium such as liquid mercury (or through a wire) to briefly store data. As series of acoustic pulses is sent along a tube; after a time, as the pulse reached the end of the tube, the circuitry detected whether the pulse represented a 1 or 0 and caused the oscillator to re-send the pulse. Others used Williams tubes, which use the ability of a television picture tube to store and retrieve data. By 1954, magnetic core memory[2] was rapidly displacing most other forms of temporary storage, and dominated the field through the mid-1970s.

The first working von Neumann machine was the Manchester "Baby" or Small-Scale Experimental Machine, developed by Frederic C. Williams and Tom Kilburn and built at the University of Manchester in 1948;[3] it was followed in 1949 by the Manchester Mark I computer which functioned as a complete system using the Williams tube and magnetic drum for memory, and also introduced index registers.[4] The other contender for the title "first digital stored program computer" had been EDSAC, designed and constructed at the University of Cambridge. Operational less than one year after the Manchester "Baby", it was also capable of tackling real problems. EDSAC was actually inspired by plans for EDVAC (Electronic Discrete Variable Automatic Computer), the successor to ENIAC; these plans were already in place by the time ENIAC was successfully operational. Unlike ENIAC, which used parallel processing, EDVAC used a single processing unit. This design was simpler and was the first to be implemented in each succeeding wave of miniaturization, and increased reliability. Some view Manchester Mark I / EDSAC / EDVAC as the "Eves" from which nearly all current computers derive their architecture.

The first universal programmable computer in the Soviet Union was created by a team of scientists under direction of Sergei Alekseyevich Lebedev from Kiev Institute of Electrotechnology, Soviet Union (now Ukraine). The computer MESM (МЭСМ, Small Electronic Calculating Machine) became operational in 1950. It had about 6,000 vacuum tubes and consumed 25 kW of power. It could perform approximately 3,000 operations per second. Another early machine was CSIRAC, an Australian design that ran its first test program in 1949. CSIRAC is the oldest computer still in existence and the first to have been used to play digital music.[5]
In October 1947, the directors of J. Lyons & Company, a British catering company famous for its teashops but with strong interests in new office management techniques, decided to take an active role in promoting the commercial development of computers. By 1951 the LEO I computer was operational and ran the world's first regular routine office computer job.
Manchester University's machine, also a Mark I became the prototype for the Ferranti Mark I. The first Ferranti Mark I machine was delivered to the University in February, 1951 and at least nine others were sold between 1951 and 1957.

In June 1951, the UNIVAC I (Universal Automatic Computer) was delivered to the U.S. Census Bureau. Remington Rand eventually sold 46 machines at more than $1 million each. UNIVAC was the first 'mass produced' computer; all predecessors had been 'one-off' units. It used 5,200 vacuum tubes and consumed 125 kW of power. It used a mercury delay line capable of storing 1,000 words of 11 decimal digits plus sign (72-bit words) for memory. Unlike IBM machines it was not equipped with a punch card reader but 1930s style metal magnetic tape input, making it incompatible with some existing commercial data stores. High speed punched paper tape and modern-style magnetic tapes were used for input/output by other computers of the era.
In November 1951, the J. Lyons company began weekly operation of a bakery valuations job on the LEO (Lyons Electronic Office). This was the first business application to go live on a stored program computer.

In 1952, IBM publicly announced the IBM 701 Electronic Data Processing Machine, the first in its successful 700/7000 series and its first IBM mainframe computer. The IBM 704, introduced in 1954, used magnetic core memory, which became the standard for large machines. The first implemented high-level general purpose programming language, Fortran, was also being developed at IBM for the 704 during 1955 and 1956 and released in early 1957. (Konrad Zuse's Plankalkül language was designed in 1945 but had not yet been implemented in 1957.)

IBM introduced a smaller, more affordable computer in 1954 that proved very popular. The IBM 650 weighed over 900 kg; the attached power supply weighed around 1350 kg and both were held in separate cabinets of roughly 1.5 meters by 0.9 meters by 1.8 meters. It cost $500,000 or could be leased for $3,500 a month. Its drum memory was originally only 2000 ten-digit words, and required arcane programming for efficient computing. Memory limitations such as this were to dominate programming for decades afterward, until the evolution of hardware capabilities which allowed the development of a programming model that could be more sympathetic to software development.[6]
In 1955, Maurice Wilkes invented microprogramming,[7] which was later widely used in the CPUs and floating-point units of mainframe and other computers, such as the IBM 360 series. Microprogramming allows the base instruction set to be defined or extended by built-in programs (now sometimes called firmware, microcode, or millicode).
In 1956, IBM sold its first magnetic disk system, RAMAC (Random Access Method of Accounting and Control). It used 50 24-inch (610 mm) metal disks, with 100 tracks per side. It could store 5 megabytes of data and cost $10,000 per megabyte. (As of 2008, magnetic storage, in the form of hard disks, costs less than one 50th of a cent per megabyte).
- There is an uncomfortable point here: when we (as a civilization) find a successful direction, how can we be sure that we are not going off-track? (as in the rain dance). Some examples:
- (1) just because something feels right we do it (right here in Wisconsin) when it fits our belief system.
- (2) we follow our ideologies -- The Chief Speaker, Moctezuma_II, of the Aztec civilization destroyed it when a prediction he expected seemed to come true, right down to the expected year (One Reed in the Aztec calendar which is 1519 in the Gregorian calendar), as foretold in the Aztec tradition. The Aztecs collide with the Spaniards, and are conquered in the years to follow, by technology (stone age vs. iron age), smallpox, and religion (Huitzilopochtli vs. the Reconquista). 07:30, 29 April 2008 (UTC)
- I quote your statement "The validity of a theory is decided by scientists who interpret data". The Stern-Gerlach experiment was a surprise to those who were trained to interpret data with classical theory, as the results do not fit the classical picture. How is that not a black swan case?
- Avoiding the fallacy of 'affirming the consequent as proof' need not require the philosophical position of falsificationism as part of scientific method, if that is your entire point. I do not disagree that falsificationism is not required. However, the psychological lift of seeing a hypothesized condition actually appear is an undeniable part of both scientific method and mathematical analysis. --Ancheta Wis (talk) 21:34, 26 January 2008 (UTC)

- Let's share some common experience here, so that it becomes easier to communicate. From the article, there is a picture which illustrates a sentence, "Elsie the cat is sitting on a mat". One possible abstraction of that sentence, "Cat on mat", is pretty much reduced to two nouns linked by a preposition. Now the good thing about abstraction is that it becomes possible to communicate the point of a sentence. Now if you were concerned about your mat then you might have an interest in getting that cat off your mat. But if I were concerned about my cat, who had disappeared for two weeks, and we had the cat in front of us, as in the picture, then I might be interested in luring that cat back home.
- In this hypothetical case, we are both concerned about where that darn cat is, for our own reasons, and graphic evidence serves us both well. —Preceding unsigned comment added by Ancheta Wis (talk • contribs) 02:28, 1 January 2008 (UTC)
- When Newton wrote Principia he didn't sleep or eat for days on end. When Galileo looked at the sun thru his telescope, he did damage to his eyes and went blind eventually. When Einstein went thru his divorce he promised the money from his Nobel prize as part of the settlement; he was so sure he would get the prize, he made the promise beforehand. These facts are well known. I would guess that many others are similarly passionate about their commitments as well. Alhacen said it best: Truth is sought for its own sake. And those who are engaged upon the quest for anything for its own sake are not interested in other things. Finding the truth is difficult, and the road to it is rough. You don't get the same commitment to truth if your POV is pragmatic, because at the slightest difficulty, you will give up in favor of an expedient. Here is a more recent example: in the Japanese invasion of the Philippines, the Japanese would torture to get information. One American officer simply responded to the torture with a grin. In exasperation, they bayoneted him to death. Thus that officer was more committed than his torturers were. The officer 'won', you might say. --Ancheta Wis (talk) 17:46, 22 December 2007 (UTC)
In WWII, Russell Volckmann was a US Army officer who retreated to the Cordillera of Northern Luzon, Philippines. His 1954 memoir We Remained is online. A handful of American officers remained to lead the guerilla operation. They actually remained in radio contact with Brisbane (MacArthur headquarters during the war. He was resupplied by submarine after arduous effort and careful planning before the invasion. --Ancheta Wis (talk) 11:59, 28 November 2007 (UTC)
I just noted your reversion on the article page. Perhaps all the quotations from Popper might stand on their own to face just what the readers might decide, on the worth of what Popper has said, in the face of his published self-contradictions. After all, you can prove anything from a contradiction. That's why Alan Turing quit attending Wittgenstein's classes. --Ancheta Wis (talk) 12:41, 26 November 2007 (UTC)
The Genesis and Development of a Scientific Fact was written by Ludwik Fleck (1896-1961), a Polish physician. Fleck published the German edition in 1935: Entstehung und Entwicklung einer wissenschaftlichen Tatsache. Einführung in die Lehre vom Denkstil und Denkkollektiv, Schwabe und Co., Verlagsbuchhandlung, Basel.
The first English translation, The Genesis and Development of a Scientific Fact, was translated and edited by T.J. Trenn and R.K. Merton, foreword by Thomas Kuhn, and published by Chicago: University of Chicago Press, 1979.
Fleck's case history of the discovery of the Wassermann reaction to syphilis, was originally published in German in 1935, and republished in English in 1979 after having been cited by Thomas Kuhn as an important influence on his own conception of the history of science. Both Fleck's history of discovery, and the history of his book's re-discovery, exemplify a view of progress that continues to inform research in the science and technology studies fields.
The book[edit]
Kuhn writes "Fleck is concerned with ... the personal, tentative, and incoherent character of journal science together with the essential and creative act of the individuals who add order and authority by selective systematization within a vademecum."[8]
"Wissen ist Macht und soll für jedermann frei verfügbar sein."
In my opinion, the article is now beginning to tell a story, by showing more of the interconnection between the theories. In the age of Newton, we could model physics as hard spheres, sometimes with rigid rods connecting the spheres. This view held, up to the age of Maxwell. But once it was discovered that these spheres could have structure, with properties like charge or spin, then their motion could explain not only the emission of light, but also the absorption of light and other energy. By investigating these physical properties, physicists could then begin to investigate the properties of matter at ever higher energies, at ever colder temperatures, as well as for other properties, like size. This allows a picture of physics where the bodies under discussion are no longer hard spheres, but which can deform, spread (and perhaps entangle) and further alter their physical properties, during the propagation and transmission of energy in the system under consideration. --Ancheta Wis 08:56, 10 October 2007 (UTC)
I just learned about this medication last night in conversation; as I have a friend who suffers migraine headaches, my attention was roused. As it was described to me, loss of patience can be a side-effect. One of the fascinating side-effects, after the medication was begun, was an increase in rage at others, including strangers. Apparently, if you work at a help desk or other people-contact jobs, you ought not to take topamax and work customer service for three to four months until your body learns how to deal with the topamax. --Ancheta Wis 12:38, 30 September 2007 (UTC)
http://wikidashboard.parc.com/w/index.php?title=Special:Userlogin&returnto=Help:Contents
open proxy: IP address for Wikidashboard: http://wikidashboard.parc.com
Your IP address is 209.233.50.75, and your block has been set to expire: indefinite. —Preceding unsigned comment added by Ancheta Wis (talk • contribs) 09:34, 22 September 2007 (UTC)
"And if thine eye offend thee, pluck it out..." --Mark 9:47
It is inconsistent to criticize the History for length, and then to pluck it out for yet another reason. There is no limit to the number of names in a history, and yet one can make the case for the founder of a science. That would be Newton. Galileo has been called the Father of Modern Science, and Kepler spent ths twenty years on his laws, which Newton was able to derive, per the quote #3. Copernicus goes a little farther with his heliocentric system, but then you have to include Yajnavalkya, Aristarchus, al-Biruni, Alhacen etc. in the millennia before that. If we include Maxwell, then we have to include Faraday, and before him Oersted and before him Ritter, Benjamin Franklin, Volta, Galvani, Gilbert etc. If we include Einstein we have to include Mach, Lorentz, Poincaré etc. If we include Schrödinger we have to include Heisenberg and Born and Ehrenfest.
If we limit this to a history of ideas, that would make a case for Galileo, Newton, Orsted, Faraday, Maxwell, Planck, Einstein. If I limited that to one quote apiece that is still a section which is 3x longer than the above. --Ancheta Wis 00:36, 23 September 2007 (UTC)
While editing the history section I was struck how Newton used underlying models for his science. Thus mechanics serves as a thin veneer over a mathematical model with equations serving to explain a System of the World. And we learn these approximations in school. So matter is a collection of particles, or rigid bodies, or unstretchable strings, etc. This leads to egregious designs like Galloping Gertie, where rigid bodies had to give way to more flexible structures.
This brings me to a pet peeve. What's the big deal about 'matter'? It reeks of the 4 humours or the 4 causes of Aristotle. It is a 'mass noun' which allows us to sweep detail under the rug of a model. Why are we compelled to mention matter as something real? It strikes me as a false fundamental. Why not just live with the equations, give their subjects names, and work with the resultant propositions? For example, why don't we just talk about particles which obey Fermi statistics, or Bose-Einstein statistics, and skip the mythical point endowed only with mass.
This has implications for the article. The so-called 'core theories' can be learned with the abstract definitions, but the real items which are the subject of experiment have lots of messy properties, like the magnets which have disturbed the experimental schedule of the collider at CERN. And you have the spectacle of students of physics who have partial understanding of one or two fields. What comes to mind are the critics of the GPS system who think that you can design them without the relativistic corrections. --Ancheta Wis 02:00, 20 September 2007 (UTC)
History[edit]
Inquiry into the nature of matter dates from at least several thousand years ago, from the civilizations of the Fertile Crescent to the Hellenes. philosophical terms, and never verified by systematic experimental testing as is popular today. The works of Ptolemy and Aristotle however, were also not always found to match everyday observations. There were exceptions and there are anachronisms: for example, Indian philosophers and astronomers gave many correct descriptions in atomism and astronomy, and the Greek thinker Archimedes derived many correct quantitative descriptions of mechanics and hydrostatics.
The willingness to question previously held truths and search for new answers eventually resulted in a period of major scientific advancements, now known as the Scientific Revolution of the late 17th century. The precursors to the scientific revolution can be traced back to the important developments made in India and Persia, including the elliptical model of the planets based on the heliocentric solar system of gravitation developed by Indian mathematician-astronomer Aryabhata; the basic ideas of atomic theory developed by Hindu and Jaina philosophers; the theory of light being equivalent to energy particles developed by the Indian Buddhist scholars Dignāga and Dharmakirti; the optical theory of light developed by Persian scientist Alhazen; the Astrolabe invented by the Persian Mohammad al-Fazari; and the significant flaws in the Ptolemaic system pointed out by Persian scientist Nasir al-Din al-Tusi. As the influence of the Islamic Caliphate expanded to Europe, the works of Aristotle preserved by the Arabs, and the works of the Indians and Persians, became known in Europe by the 12th and 13th centuries.
The Scientific Revolution[edit]

The Scientific Revolution is held by most historians (e.g., Howard Margolis) to have begun in 1543, when the first printed copy of Nicolaus Copernicus's De Revolutionibus (most of which had been written years prior but whose publication had been delayed) was brought to the influential Polish astronomer from Nuremberg.

Further significant advances were made over the following century by Galileo Galilei, Christiaan Huygens, Johannes Kepler, and Blaise Pascal. During the early 17th century, Galileo pioneered the use of experimentation to validate physical theories, which is the key idea in modern scientific method. Galileo formulated and successfully tested several results in dynamics, in particular the Law of Inertia. In 1687, Newton published the Principia, detailing two comprehensive and successful physical theories: Newton's laws of motion, from which arise classical mechanics; and Newton's Law of Gravitation, which describes the fundamental force of gravity. Both theories agreed well with experiment. The Principia also included several theories in fluid dynamics. Classical mechanics was re-formulated and extended by Leonhard Euler, French mathematician Joseph-Louis Comte de Lagrange, Irish mathematical physicist William Rowan Hamilton, and others, who produced new results in mathematical physics. The law of universal gravitation initiated the field of astrophysics, which describes astronomical phenomena using physical theories.
After Newton defined classical mechanics, the next great field of inquiry within physics was the nature of electricity. Observations in the 17th and 18th century by scientists such as Robert Boyle, Stephen Gray, and Benjamin Franklin created a foundation for later work. These observations also established our basic understanding of electrical charge and current.

In 1821, the English physicist and chemist Michael Faraday integrated the study of magnetism with the study of electricity. This was done by demonstrating that a moving magnet induced an electric current in a conductor. Faraday also formulated a physical conception of electromagnetic fields. James Clerk Maxwell built upon this conception, in 1864, with an interlinked set of 20 equations that explained the interactions between electric and magnetic fields. These 20 equations were later reduced, using vector calculus, to a set of four equations by Oliver Heaviside.

In addition to other electromagnetic phenomena, Maxwell's equations also can be used to describe light. Confirmation of this observation was made with the 1888 discovery of radio by Heinrich Hertz and in 1895 when Wilhelm Roentgen detected X rays. The ability to describe light in electromagnetic terms helped serve as a springboard for Albert Einstein's publication of the theory of special relativity in 1905. This theory combined classical mechanics with Maxwell's equations. The theory of special relativity unifies space and time into a single entity, spacetime. Relativity prescribes a different transformation between reference frames than classical mechanics; this necessitated the development of relativistic mechanics as a replacement for classical mechanics. In the regime of low (relative) velocities, the two theories agree. Einstein built further on the special theory by including gravity into his calculations, and published his theory of general relativity in 1915.
One part of the theory of general relativity is Einstein's field equation. This describes how the stress-energy tensor creates curvature of spacetime and forms the basis of general relativity. Further work on Einstein's field equation produced results which predicted the Big Bang, black holes, and the expanding universe. Einstein believed in a static universe and tried (and failed) to fix his equation to allow for this. However, by 1929 Edwin Hubble's astronomical observations suggested that the universe is expanding.
From the late 17th century onwards, thermodynamics was developed by physicist and chemist Boyle, Young, and many others. In 1733, Bernoulli used statistical arguments with classical mechanics to derive thermodynamic results, initiating the field of statistical mechanics. In 1798, Thompson demonstrated the conversion of mechanical work into heat, and in 1847 Joule stated the law of conservation of energy, in the form of heat as well as mechanical energy. Ludwig Boltzmann, in the 19th century, is responsible for the modern form of statistical mechanics.
1900 to Present[edit]
In 1895, Röntgen discovered X-rays, which turned out to be high-frequency electromagnetic radiation. Radioactivity was discovered in 1896 by Henri Becquerel, and further studied by Marie Curie, Pierre Curie, and others. This initiated the field of nuclear physics.
In 1897, Joseph J. Thomson discovered the electron, the elementary particle which carries electrical current in circuits. In 1904, he proposed the first model of the atom, known as the plum pudding model. (The existence of the atom had been proposed in 1808 by John Dalton.)
These discoveries revealed that the assumption of many physicists that atoms were the basic unit of matter was flawed, and prompted further study into the structure of atoms.
In 1911, Ernest Rutherford deduced from scattering experiments the existence of a compact atomic nucleus, with positively charged constituents dubbed protons. Neutrons, the neutral nuclear constituents, were discovered in 1932 by Chadwick. The equivalence of mass and energy (Einstein, 1905) was spectacularly demonstrated during World War II, as research was conducted by each side into nuclear physics, for the purpose of creating a nuclear bomb. The German effort, led by Heisenberg, did not succeed, but the Allied Manhattan Project reached its goal. In America, a team led by Fermi achieved the first man-made nuclear chain reaction in 1942, and in 1945 the world's first nuclear explosive was detonated at Trinity site, near Alamogordo, New Mexico.
In 1900, Max Planck published his explanation of blackbody radiation. This equation assumed that radiators are quantized in nature, which proved to be the opening argument in the edifice that would become quantum mechanics. Beginning in 1900, Planck, Einstein, Niels Bohr, and others developed quantum theories to explain various anomalous experimental results by introducing discrete energy levels. In 1925, Heisenberg and 1926, Schrödinger and Paul Dirac formulated quantum mechanics, which explained the preceding heuristic quantum theories. In quantum mechanics, the outcomes of physical measurements are inherently probabilistic; the theory describes the calculation of these probabilities. It successfully describes the behavior of matter at small distance scales. During the 1920s Erwin Schrödinger, Werner Heisenberg, and Max Born were able to formulate a consistent picture of the chemical behavior of matter, a complete theory of the electronic structure of the atom, as a byproduct of the quantum theory.
Quantum field theory was formulated in order to extend quantum mechanics to be consistent with special relativity. It was devised in the late 1940s with work by Richard Feynman, Julian Schwinger, Sin-Itiro Tomonaga, and Freeman Dyson. They formulated the theory of quantum electrodynamics, which describes the electromagnetic interaction, and successfully explained the Lamb shift. Quantum field theory provided the framework for modern particle physics, which studies fundamental forces and elementary particles.
Chen Ning Yang and Tsung-Dao Lee, in the 1950s, discovered an unexpected asymmetry in the decay of a subatomic particle. In 1954, Yang and Robert Mills then developed a class of gauge theories which provided the framework for understanding the nuclear forces. The theory for the strong nuclear force was first proposed by Murray Gell-Mann. The electroweak force, the unification of the weak nuclear force with electromagnetism, was proposed by Sheldon Lee Glashow, Abdus Salam and Steven Weinberg and confirmed in 1964 by James Watson Cronin and Val Fitch. This led to the so-called Standard Model of particle physics in the 1970s, which successfully describes all the elementary particles observed to date.
Quantum mechanics also provided the theoretical tools for condensed matter physics, whose largest branch is solid state physics. It studies the physical behavior of solids and liquids, including phenomena such as crystal structures, semiconductivity, and superconductivity. The pioneers of condensed matter physics include Bloch, who created a quantum mechanical description of the behavior of electrons in crystal structures in 1928. The transistor was developed by physicists John Bardeen, Walter Houser Brattain and William Bradford Shockley in 1947 at Bell Telephone Laboratories.
right|130px The two themes of the 20th century, general relativity and quantum mechanics, appear inconsistent with each other. General relativity describes the universe on the scale of planets and solar systems while quantum mechanics operates on sub-atomic scales. This challenge is being attacked by string theory, which treats spacetime as composed, not of points, but of one-dimensional objects, strings. Strings have properties like a common string (e.g., tension and vibration). The theories yield promising, but not yet testable results. The search for experimental verification of string theory is in progress.
The United Nations declared the year 2005, the centenary of Einstein's annus mirabilis, as the World Year of Physics.
George Polya's four steps for constructing a mathematical proof[9] differ from scientific method in both purpose and detail, and yet the process of analysis requires the ability to make conjectures (to guess) as in the second step of scientific method.
Introduction to scientific method[edit]
Alhacen (Ibn Al-Haytham 965 – 1039, a pioneer of scientific method) on truth: "Truth is sought for its own sake. And those who are engaged upon the quest for anything for its own sake are not interested in other things. Finding the truth is difficult, and the road to it is rough. ..." [10]
"How does light travel through transparent bodies? Light travels through transparent bodies in straight lines only. ... We have explained this exhaustively in our Book of Optics. But let us now mention something to prove this convincingly: the fact that light travels in straight lines is clearly observed in the lights which enter into dark rooms through holes. ... the entering light will be clearly observable in the dust which fills the air." -- Alhacen[11]
Alhacen's conjecture: "Light travels through transparent bodies in straight lines only".
Alhacen's corroboration: Place a straight stick or a taut thread next to the light, to prove that light travels in a straight line.
Truth and myth[edit]
A myth need not be true (although a myth can be true); when constructing a generalization from a set of observations, it is necessary to disprove its contrapositive, by the laws of logic. It is a fallacy to continually reify a statement as proof of a generalization.
Some examples of incorrect generalization based on observation alone include:
- To make houseflies, hang a piece of raw meat from the eaves of your house.
- To make mice, pile dirty clothes in the corner of your room.
- To fall off the edge of the earth, sail west from the Mediterranean Sea through the pillars of Hercules into the Ocean.
The crucial experiment will distinguish whether a generalization is correct or not. —Preceding unsigned comment added by Ancheta Wis (talk • contribs) 15:42, 3 September 2007 (UTC)
A conundrum[edit]
Kenosis, I propose a rewrite of the initial part of the article, based on a conundrum, meaning a question whose answer is a conjecture, a question, or a riddle. The reason is that scientific method excels at the discovery of new knowledge, and it is here that we can best expose its advantages.
Here is a proposed outline. I hope to draw in other editors so that we can take advantage of the wiki-action, and have fun updating the article to increase its rating.
- 1. A sample question. We could start with something which was not known, say, at the beginning of the development of scientific method, with Alhacen's book on optics, for example. We then use Alhacen's experiment to show that light travels in a straight line. This may seem obvious now, but it was not understood a millennium ago. My reference will be Alhacen's experiment with a camera oscura (which has more than a passing resemblance to Newton's experiment with a prism, 320 years ago).
- 1.1 This includes Observation, Description, and Conjecture (hypothesis).
- 1.2 Alhacen's experiment includes Prediction, Control, Identification, and Variation etc.
- 1.3 The provisional nature of the Conjecture can be highlighted by displaying the various provisional explanations and controversy.
- 1.4
- 2. Another question, possibly a more recent one, with an answer which is not generally accepted or controversial (a more recent conundrum)
- 2.1 Wien Black-body radiation
- 2.2 Quanta
- 2.3 Photons
- 2.4 Quantum entanglement
- 3. A classical question and its famous answer: for example, the nature of matter and the atomic hypothesis
- 3.1 Thales
- 3.2 Democritus
- 3.3 Dalton
- 3.4 Mendeleev
- 4. Another question, possibly from the 20th century, with an answer which is well established, but not so famous except to those in the know: for example, the unification of black holes, gravitation, and quantum theory by Hawking
- 4.1 Newton
- 4.2 Einstein
- 4.3 Black Holes
- 4.4 Hawking
- 5. An application, say from business or commerce.
- 5.1 Industrialization
- 5.2 Investment
- 5.3 Insurance
- 5.4 Risk
Ancheta Wis 03:42, 12 September 2007 (UTC)
- ^ John von Neumann (1945), First Draft of a Report on the EDVAC
- ^ U.S. Patent 2,708,722 "Pulse transfer controlling devices", An Wang filed October 1949, issued May 1955
- ^ Enticknap, Nicholas (Summer 1998). "Computing's Golden Jubilee". RESURRECTION (20). The Computer Conservation Society. ISSN 0958-7403. Retrieved 2008-04-19.
- ^ Computer History Museum, Manchester Mark I
- ^ "CSIRAC: Australia's first computer". Retrieved 2007-12-21.
- ^ The hardware capability which provides a better software development environment includes a large, linear memory model, rapid execution of programs within seconds of time, multiprogramming, full-screen editing, and, some would say, a GUI. FORTRAN and COBOL have a static memory model; C has a frame-based memory model.
- ^ Maurice Wilkes, Memoirs of a Computer Pioneer. The MIT Press. 1985. ISBN 0-262-23122-0
- ^ p. ix, Thomas Kuhn's foreword to Fleck's Genesis and Development of a Scientific Fact ISBN 0-226-25325-2
- ^
- 1. "You have to understand the problem."
- 2. (Analysis) "Make a plan."
- 3. (Synthesis) "Carry out the plan."
- 4. "Look back."
- ^ Alhazen (Ibn Al-Haytham) Critique of Ptolemy, translated by S. Pines, Actes X Congrès internationale d'histoire des sciences, Vol I Ithaca 1962, as referenced on p.139 of Shmuel Sambursky (ed. 1974) Physical Thought from the Presocratics to the Quantum Physicists ISBN 0-87663-712-8
- ^ Alhazen, translated into English from German by M. Schwarz, from "Abhandlung über das Licht", J. Baarmann (ed. 1882) Zeitschrift der Deutschen Morgenländischen Gesellschaft Vol 36 as referenced on p.136 by Shmuel Sambursky (1974) Physical thought from the Presocratics to the Quantum Physicists ISBN 0-87663-712-8
- New Century Financial Corporation,
- Countrywide Financial Corp.,
- Ameriquest Mortgage,
- HSBC Holdings
- Fremont General Corp.
- SouthStar Funding, LLC bankrupt
- Homebanc Mortgage
- H&R Block Inc.
- The Bear Stearns Companies, Inc. announced that it is preparing to shut down two hedge funds, Bear's High-Grade Structured Credit Strategies Enhanced Leverage Fund and High Grade Structured Credit Strategies Fund.
In the table of the distribution of world religions, I was surprised to see no mention of Animism, or the belief that animal species can be totems of religion. Thus belief that turtles or birds, for example, might signify some good thing, like storks in northern Europe. This type of belief can be just as valid as ism as a folk religion. My motivation is the beliefs of the American Pacific Northwest tribes, as documented in museums like the Field Museum. The exhibit used to hold some items which the Native Americans of the Pacific Northwest hold sacred(I believe they were masks of animals, such as bears or birds ). Those items are no longer displayed, and were even returned by the Museum. (Other sacred practices include worship of Pele in Hawaii, etc.)
When I follow the link to ism, I am surprised to see that the term has a Christian connotation/usage, much like the Gentile appellation in Jewish usage. Might this use of the term ism not be a signal of some type of bias in the selection of the category or class of religion?
I am further surprised that Animism is flagged as being a non-neutral article. Why might this be so, especially since Animism neatly explains many of the beliefs of the Native American people. I am even inclined to call these beliefs religious beliefs, and worthy of inclusion in the table of religions. For example, a mountain visible from my home town, Sierra Blanca, is sacred to the Mescalero Apache. In fact, they operate a hotel called the Inn of the Mountain Gods, referring directly to the mountain of which I speak. And if that is to be dismissed as marketing hype, how do we reconcile this with the historical practice and usage of traditional dances, which were at first suppressed by the padres (but later allowed, and which survive to this day).
Failing that, why not label the subject of the term ' ism' as folk religion instead? That would avoid the animism onus, if that is a non-neutral term. I am not an expert on the subject, but it seems inherently unfair that the Pueblo People's indigenous religions, or the Apache's indigenous religion might not be included in some category of the listed table. Now that I have followed the link to 'Folk religion' I see that it does not qualify on an institutional basis, such as an Army or a Navy. (I refer of course to the quip that a language is a dialect with an army and a navy.)
Again, the articles seem unfair and biased. If any of this is naive, I stand corrected. But I await an explanation in the articles. --Ancheta Wis 09:56, 1 July 2007 (UTC)
Stephen Toulmin (1967) "The Astrophysics of Berossos the Chaldean", Isis, Vol. 58, No. 1 (Spring, 1967), pp. 65-76 [1]
European Neural Network Society 2002
Google radar Bayes Kolmogorov signal processing Wiener filter Google counterfactual epistemic probability defeasible
George E. P. Box (1978) Statistics for Experimenters ISBN 0-471-09315-7
In the past few centuries, some statistical methods have been developed, for reasoning in the face of uncertainty, as an outgrowth of methods for eliminating error. This was an echo of the program of Francis Bacon's Novum Organum. Bayesian inference acknowledges one's ability to alter one's beliefs in the face of evidence. This has been called belief revision, or defeasible reasoning: the models in play during the phases of scientific method can be reviewed, revisited and revised, in the light of further evidence. This arose from the work of Frank P. Ramsey[1], John Maynard Keynes[2], and earlier, William Stanley Jevons' work[3] in economics. ; one's individual actions Alan Hájek, "Scotching Dutch Books?" Philosophical Perspectives 19 Per Gunnar Berglund, "Epistemic Probability and Epistemic Weight" The rise of Bayesian probability
- The deviation from truth was first quantified two centuries ago, by mathematical modeling of error as the deviation from the mean of a normal distribution of observations. Gauss used this approach to prove his method of least squares, which he used to predict the position of the asteroid Ceres. A normal distribution (or gaussian) might then be used to characterize error in observations. William Gosset's, or Student's t is a well-known statistic for error. Other probability distributions have been formulated: the Poisson distribution (in which the standard deviation is equal to the mean), the exponential distribution, and so forth. Gauss' techniques may well be used to monitor the close encounter of Earth with asteroid Apophis on April 13, 2036. The current probability of hitting our planet on this date is 1 in 45,0000.
- Originally, probability was formulated as a method for handling the risk of betting[4]. This viewpoint was systematized by decomposing its components into independent events by Andrey Kolmogorov's axioms for probability theory. [5] Statistical theory had its origins in probability. Karl Pearson (1857 – 1936) established mathematical statistics along with other important contributors to statistics. Inferential statistics textbook
- In a parallel effort, Leibniz, Pascal, Babbage and Jevons' algorithmic thinking stimulated the development of mechanical computing, which gave rise to entire classes of professional careers. Before the mid-twentieth century, computer was a person's job title; women were able to pursue professional careers as computers, at a time when other professions were unavailable to them, before the rise of computing hardware in the mid-twentieth century.
These statistical and algorithmic approaches to reasoning embed the phases of scientific method within their theory, including the very definition of some fundamental concepts.
- Thomas Bayes (1702 — 1761) started a method of thinking (defeasible reasoning) which acknowledges that our concepts can evolve from some ideal expectation to some actual result. In the process of learning some condition, our concepts can then keep pace with the actual situation. Unlike classical logic, in which propositions are evaluated true, false, or undecided, a Bayesian thinker would assign a conditional probability to to a proposition. This is called Bayesian inference: "The sun has risen for billions of years. The sun rose today. With high probability, the sun will rise tomorrow.".
- Frank Plumpton Ramsey (1903-1930) formulated a practice, conveniently understood by betting. In this practice (known as the pragmatic theory of truth), one assigns a probability, as a measure of partial belief in a subjective statement, to a subjective proposition which one, as the interested individual, can understand best. Ramsey thus provided a foundation for Bayesian probability, which is a direct method for assigning posterior probabilities to any number of hypotheses directly. See Ramsey biography, Ramsey theory. [6]
- In the past 50 years, machines have been built which utilize this type of theory. (See for example Dempster-Shafer theory.) This method rests on the notion of prior and posterior probabilities of a situation or event. A prior probability is assigned prior to an event's occurrence or known existence, while a posterior probability is to be assigned after an event is known.
- In statistical theory, experimental results are part of sample space, as are observations. estimation theory to process observations, perhaps in multiple comparisons. Signal processing can then be used to extract more information from observations.
- hypothesis testing, part of mathematical statistics. decision theory can be used in the design of experiments to select hypotheses using a test statistic Omnibus test Behrens-Fisher problem Bootstrapping (statistics) Falsifiability
- design of experiments Ronald Fisher (1890 – 1962) Maximum likelihood estimation Fisher's method for combining independent tests of significance level α Statistical significance Null hypothesis Type I error, Type II error confidence level over a confidence interval
- error has a corresponding place in computation; in this subject, a calculation has some error specified by the number of digits or bits in a result, with the least significant figure discounted by an error tolerance band. Even in financial fields, where an account is best known to the penny, allowance for error is made by writeoffs and losses.
- The stages of scientific method usually involve formal statements, or definitions which express the nature of the concepts under investigation. Any time spent considering these concepts will materially aid the research. For example, the time spent waiting in line at a store can be modelled by queueing theory. The clerk at the store might then be considered an agent. The owner of the store and each customer might be considered to be principals in a transaction.
In summary, scientific thought as embodied in scientific method, has moved from reliance on Platonic ideal, with logic and truth as the sole criterion, to its current place, centrally embedded in statistical thinking, where some model or theory is evaluated by random variables, which are mappings of experiment results to some mathematical measure, all subject to uncertainty, with an explicit error.
- ^ A review and defense of Frank P.Ramsey's formulation can be found in [2]
- ^ John Maynard Keynes(1921) Treatise on Probability
- ^ William Stanley Jevons(1888) The Theory of Political Economy
- ^ "Probability is best defined by betting" -- R.P. Feynman
- ^ Kolmogorov (1903 - 1987) thus influenced William Feller, (1950, 1957, 1968) An Introduction to Probability Theory and Its Applications, Volume 1 ISBN 0-471-25708-7. Feller was the chief popularizer of the Kolmogorov theory in the West for a time.
- ^ Ercan Engin Kuruoglu "Bayesian Signal Processing" http://64.233.167.104/search?q=cache:cGgX_X_XJd8J:www.busim.ee.boun.edu.tr/~busim/bayes/Bayes_Introduction.ppt+subjectivist+axiom+of+probability&hl=en&ct=clnk&cd=4&gl=us&client=firefox-a


